Вибрационный датчик относится к классу прецизионных приборов, характеризуемых уменьшением геометрических и массовых характеристик; большой концентрацией физических процессов в ограниченном объеме, уменьшением допусков на функциональные характеристики.
Функциональные характеристики вибрационного датчика имеют случайный характер. Вариации характеристик определяются: исполнителем работ; допуском на геометрические размеры; сырьем и исходными материалами; технологическим процессом; оборудованием и инструментом; средствами и методами измерения результатов; окружающей средой.
Улучшение качества и уменьшение количества несоответствий при выпуске датчиков достигается не ужесточением требований к системе и увеличением вариаций случайных параметров, а уменьшением вариаций результатов деятельности, считая, что качество формирует технологический процесс.
Цель исследования – определить рациональные границы допусков на геометрические размеры с учетом свойств материала и уменьшить вариации функциональных характеристик датчика, обеспечив увеличение числа выхода годных датчиков при производстве.
Известные методы повышения эффективности производства не в полной мере позволяют получить существенный результат в решении задачи определения требуемых функциональных характеристик приборов. Использование информационных систем проведения динамического анализа поможет контролировать связь между функциональными характеристиками датчика, конструктивными параметрами и параметрами технологического процесса.
Материал и методы исследования
Анализ поперечных колебаний чувствительного элемента вибрационного датчика. В качестве модели чувствительного элемента используется струна либо стержень.
Результаты исследования и их обсуждение
Результаты работы могут быть использованы при конструировании датчиков для определения критичных конструктивных параметров и при их изготовлении для определения параметров технологического процесса.
Научная новизна
Решенные новые задачи по анализу частоты колебаний доведены до числового результата и позволяют оценить влияние допусков на геометрические размеры; влияние магнитного поля, случайного характера геометрических размеров на функциональные характеристики датчика.
Предложенная концепция информационной системы проведения динамического анализа включает несколько модулей: модуль механических и магнитных свойств материала, модуль конструктивных параметров (допуски на геометрические размеры, шероховатость поверхности, зазоры между деталями, размерные цепи); модуль аналитических выражений связи между конструктивными параметрами и функциональными характеристиками; модуль экспериментальных зависимостей между параметрами технологического процесса и конструктивными параметрами.
Практическое использование
Применение системного подхода к процессу производства датчиков для уменьшения вариаций параметров технологического процесса с использованием информационной системы, сокращение количества несоответствий при производстве датчиков.
Применение информационной системы позволило существенно сократить длительность технологической подготовки производства, обеспечить повышение технологичности деталей с оценкой влияния на функциональные характеристики.
При анализе влияния геометрических размеров решены вопросы:
1) разработки уточненных расчетных схем вычисления собственных частот упругой системы в статистических и динамических условиях;
2) установления связи между допуском на характеристики датчика и свойствами материала (размером зерна, легирующими элементами, модулем упругости, реологическими свойствами, режимами термообработки);
3) учета влияния внутреннего трения на частоты датчика;
4) обеспечения стабильности функциональных характеристик в зависимости от времени и температуры;
5) оценки влияния коэффициентов инерции и жесткости на функциональные характеристики.
Малые колебания струн
Уравнение малых поперечных колебаний элемента датчика – струны имеет вид [1] (рис. 1)
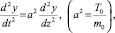 (1)
(1)
где T0 – натяжение струны, Н; m0 = bhρ – масса единицы длины струны, кг/м; (h – толщина, b – ширина, ρ – плотность). Y(z, t) – смещение произвольной точки струны.
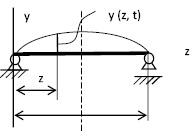
Рис. 1. Малые колебания струны
Функция Y(z, t) должна удовлетворять краевым и начальным условиям. Общее решение (1) записывается в виде
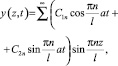 (2)
(2)
где коэффициенты C1n и C2n определяются как коэффициенты рядов Фурье для начальной формы и начального распределения скоростей точек струны.
Возможные значения частот колебаний p:
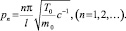 (3)
(3)
При уменьшении толщины струны с h = 0,22 мм до h = 0,19 мм (на – 13,6 %) для l = 5,7 мм частота увеличивается на +7,6 %. При той же толщине струны h = 0,220 мм увеличение длины с l = 5,7 мм до l = 5,775 мм (на + 1,3 %) приводит к уменьшению частоты на – 1,3 %. Изменение геометрических размеров с h = 0,22 мм, l = 5,7 мм до h = 0,19 мм, l = 5,775 мм вызывает увеличение частоты на +6,2 %.
При уменьшении толщины струны с h = 0,16 мм до h = 0,146 мм (на – 8,75 %) для l = 5,7 мм частота увеличивается на + 4,7 %. При той же толщине струны h = 0,16 мм увеличение длины с l = 5,7 мм до l = 5,775 мм (на +1,3 %) приводит к уменьшению частоты на – 1,3 %. Изменение геометрических размеров с h = 0,16 мм, l = 5,7 мм до h = 0,146 мм, l = 5,775 мм вызывает увеличение частоты на +6,2 %.
Уравнение малых поперечных колебаний струны при переменных по длине струны m0(z) и T0(z) имеет вид
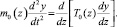 (4)
(4)
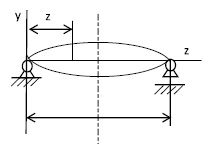
Рис. 2. Колебания струны переменного сечения
Если масса струны (масса единицы длины струны) изменяется по закону (рис. 2)
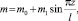 (5)
(5)
то первые две частоты колебаний, считая, что натяжение в струне Т0 при колебаниях остается практически неизменным, определяются выражениями
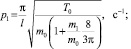 (6)
(6)
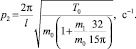 (7)
(7)
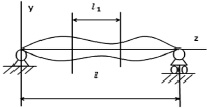
Рис. 3. Колебания струны переменного сечения
Если масса струны (масса единицы длины струны) изменяется по закону (рис. 3)
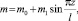 (8)
(8)
то частота колебаний определяется формулой
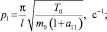 (9)
(9)
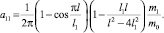
Если струна находится между полюсами N и S магнита, рис. 4, то сила притяжения со стороны магнитов при смещении струны из нейтрального положения (сила, действующая на единицу длины струны) равна [2]:
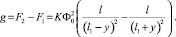
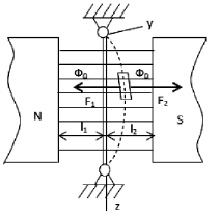
Рис. 4. Колебания струны в магнитном поле
В этом случае частоты малых колебаний:
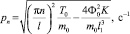 (10)
(10)
(n = 1, 2, …)
Полученные формулы используются при определении натяжения струны и оценки влияния неточности формы на частоты колебаний.
Уравнение малых поперечных колебаний элемента датчика – стержня (балки) переменного поперечного сечения (рис. 5). Имеет вид
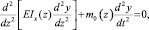 (11)
(11)
где Ix(z) – момент инерции поперечного сечения стержня.
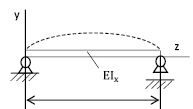
Рис. 5. Малые колебания стержня (балки)
Если EIx = const и m0(z) = const, то уравнение (11) запишется в виде
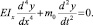 (12)
(12)
Его решение ищем в виде y(z, t) = Z(z)T(t), что позволяет получить два уравнения:
EIxZIV – m0p2Z = 0; (a)
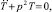 (б)
(б)
где р – частота колебаний стержня.
Решение уравнения (а) представляем в форме А.Н. Крылова:
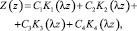
где Ki(λz) – функции Крылова, а функция Z(z) (и частоты колебаний стержня) удовлетворяет краевым условиям задачи (условиям закрепления балки).
Решение (б) записывается в виде T = C5cos pt + C6sin pt, где коэффициенты С5 и С6 определяются из начальных условий для начальной формы и начального распределения скоростей точек стержня.
Для шарнирно-опорной балки частоты колебаний определяются выражением
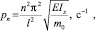
где момент инерции поперечного сечения 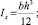 b – ширина; h – толщина стержня (h = 1, 2, …).
b – ширина; h – толщина стержня (h = 1, 2, …).
Масса единицы длины m0 = bhρ, ρ – плотность материала стержня.
С учетом этого первая частота колебаний стержня в Гц определяется выражением
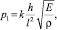 Гц,
Гц,
где k(h, E) = 1,03…1,23.
Анализ частоты упругих элементов с учетом допусков на геометрические размеры при E = 1,92∙1011 н/м2 – значение модуля упругости для сплава 45 НХТ после закалки 950 °С в воду и старении 600 °С в течение 2 ч.
b = 0,7–0,06 мм, h = 0,22–0,030 мм,
l = 5,7+0,075 мм, ρ = 8,05∙103 кг/м3.
При уменьшении толщины стержня с h = 0,22 мм до h = 0,19 мм (на – 13,6 %) для l = 5,7 мм частота уменьшается на ту же величину – 13,6 %. При толщине стержня h = 0,22 мм изменение длины с l = 5,7 мм до l = 5,775 мм (увеличение на +1,3 %) приводит к уменьшению частоты на – 2,6 %. Изменение геометрических размеров с h = 0,22 мм, l = 5,7 мм до h = 0,19 мм, l = 5,775 мм вызывает уменьшение частоты на – 15,9 %.
При уменьшении толщины стержня с h = 0,16 мм до h = 0,146 мм (на – 8,75 %) для l = 5,7 мм частота уменьшается на ту же величину – 8,75 %. При той же толщине стержня h = 0,16 мм увеличение длины с l = 5,7 мм до l = 5,775 мм (на +1,3 %) приводит к уменьшению частоты на – 2,6 %. Изменение геометрических размеров с h = 0,16 мм, l = 5,7 мм до h = 0,146 мм, l = 5,775 мм вызывает уменьшение частоты на – 11,1 %. Полученные результаты справедливы для модуля упругости E = 1,92∙1011 н/м2.
Если E = 1,82∙1011 н/м2, что соответствует старению при 700 °С, то А = 0,482∙104 Гц/м. В этом случае
а) р1 = 33625,93 Гц;
б) р1 = 29040,57 Гц (–13,6 %);
в) р1 = 32758,81 Гц (–2,6 %);
г) р1 = 28291,71 Гц (–15,9 %);
д) р1 = 29163,04 Гц;
е) р1 = 26648,47 Гц (–8,7 %);
ж) р1 = 28450,72 Гц (–2,4 %);
з) р1 = 25916,29 Гц (–11,1 %).
Полученные зависимости позволяют оценить влияние геометрических характеристик (допусков геометрических размеров) и свойств материала на частоту упругих элементов. Например, при изменении модуля упругости с E = 1,92∙1011 н/м2 до E = 1,82∙1011 н/м2 частота изменится при h = 0,22 мм, l = 5,7 мм с р1 = 34523,54 Гц до р1 = 33625,93 Гц (уменьшение на – 2,6 %); h = 0,16 мм, l = 5,7 мм с р1 = 29941,52 Гц до р1 = 29163,04 Гц (уменьшение на – 2,6 %).
Полученные зависимости частоты от геометрических размеров позволяют решить задачу в вероятностной постановке с использованием [3]. Действительно, пусть толщина стержня – случайная величина, которая подчинена нормальному закону с плотностью
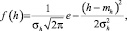 (14)
(14)
где mh, σh – математическое ожидание и среднее квадратическое отклонение толщины соответственно.
Учитывая, что частота связана с толщиной линейной зависимостью 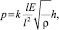 то распределение частоты также по нормальному закону с параметрами
то распределение частоты также по нормальному закону с параметрами
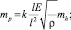 (15)
(15)
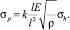 (16)
(16)
Зная закон распределения частоты, цель и допуск на цель, можно определить вероятность попадания в заданный интервал и вычислить процент брака по частоте в зависимости от допуска на геометрические размеры.
Аналогично решается задача о влиянии случайного модуля упругости на частоту.
Вычисление закона распределения частоты с учетом целевого назначения и допуска на него позволяет определить вероятность попадания служебных характеристик в заданный интервал и вычислить процент несоответствий с учетом законов распределения геометрических размеров и модуля упругости материала. В работе приведены практические рекомендации по уменьшению вариации частот – обеспечение стабильности свойств материала (модуля упругости, вязкости); электромагнитных характеристик; центра и величины рассеивания геометрических размеров; параметров электроэрозионной и электрохимической обработок, используемых для изготовления датчика.
Разработка информационной системы выполнена с использованием данных [4, 5].
Заключение
Раскрыты закономерности и проанализировано влияние параметров материала и технологического процесса на изменение частотных характеристик вибрационного датчика. Предложены рекомендации по обеспечению стабильности функциональных характеристик с учетом параметров датчика и параметров технологического процесса. Выполненные работы позволили определить рациональные границы допусков на геометрические размеры с учетом свойств материала и уменьшить вариации функциональных характеристик датчика, обеспечив увеличение числа выхода годных датчиков при производстве. На основе данных, полученных в результате проведенного анализа, были определены основные положения разработки информационной системы для проведения расчетов с целью уменьшения вариации функциональных характеристик вибрационного датчика.
Рецензенты:
Чечулин Ю.Б., д.т.н., профессор кафедры «Детали машин», Механико-машиностроительный институт, Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Паршин В.С., д.т.н., профессор, заведующий кафедрой «Металлургические и роторные машины», Механико-машиностроительный институт, Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 02.03.2015.
Библиографическая ссылка
Волкова С.Л., Воробьева И.В., Денисов Ю.В. ОСНОВНЫЕ ПОЛОЖЕНИЯ РАЗРАБОТКИ ИНФОРМАЦИОННОЙ СИСТЕМЫ ПРОВЕДЕНИЯ ДИНАМИЧЕСКОГО АНАЛИЗА ВИБРАЦИОННОГО ДАТЧИКА // Фундаментальные исследования. – 2015. – № 4. – С. 37-41;URL: https://fundamental-research.ru/ru/article/view?id=37120 (дата обращения: 27.04.2024).



