Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Езаова А.Г. 1 Думаева Л.В. 1

---

1 Кабардино-Балкарский государственный университет им. Х.М. Бербекова

Настоящая статья посвящена исследованию однозначной разрешимости одной внутренне-краевой задачи, для уравнения третьего порядка смешанного типа с группой младших членов в параболической части. В работе формулируется и доказывается теорема о существовании и единственности решения поставленной задачи. Единственность решения поставленной задачи доказывается методом интегралов энергии. Для доказательства существования решения поставленной задачи выписываются соотношения между следом искомой функции и следом производной искомой функции на линии вырождения. В параболической части поставленная задача сводится к дифференциальному уравнению третьего порядка и рассматриваются различные случаи значений коэффициентов (коэффициенты – константы, коэффициенты – функции). В случае постоянных коэффициентов выписываются три различных соотношения между следом искомой функции и следом производной искомой функции в зависимости от дискриминанта кубического уравнения, соответствующего полученному дифференциальному уравнению. В каждом из рассмотренных случаев существование решения поставленной задачи доказывается эквивалентной редукцией к интегральному уравнению Фредгольма второго рода.

Статья в формате PDF

1236 KB

краевая задача

уравнение смешанного типа

характеристики уравнения

аффиксы

метод интегралов энергии

уравнение третьего порядка

интегральное уравнение Фредгольма

операторы дробного интегро-дифференцирования

1. Езаова А.Г. Об одной нелокальной краевой задаче для уравнения смешанного третьего порядка // Известия КБГУ. – 2011. – Т 1, № 4. – С. 26–31.

2. Езаова А.Г., Водахова М.В. Задача с нелокальными условиями на характеристиках для смешанного уравнения третьего порядка // Современная математика и математическое образование, проблемы истории и философии математики: международная научная конференция Россия. – Тамбов, 2008. – С. 39–42.

3. Елеев В.А., Кумыкова С.К. О некоторых краевых задачах со смещением на характеристиках для смешанного уравнения гиперболо-параболического типа // Укр. мат. журнал. – 2000. – т. 52, № 5. – С. 707–716.

4. Нахушев А.М. Задачи со смещением для уравнений в частных производных. – М.: Наука, 2006. – 287 с.

5. Трикоми Ф. О линейных уравнениях смешанного типа. – М.: Гостехиздат, 1947.

Рассматривается уравнение

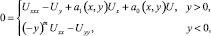(1)

где m – натуральное число, в конечной односвязной области W, ограниченной отрезками AA0, A0B0, B0B и характеристиками AC, BC уравнения (1).

Обозначим через Ω+ и Ω– части области W лежащие соответственно в полуплоскостях y > 0 и y < 0; Θ₀(x), Θ₁(x) –аффиксы точек пересечения характеристик уравнения (1), выходящих из точки (x, 0), с характеристиками AC и BC соответственно; I = АВ-интервал 0 < x < 1.

Задача. Найти функцию U(x, y) со следующими свойствами:

1)

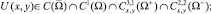
2) U(x, y) – регулярное в решение уравнения (1);

3) U(x, y) удовлетворяет краевым условиям:

U(0, y) = φ1(y); U(1, y) = φ2(y); U(0, y) = φ3(y); 0 ≤ y ≤ 1, (2)

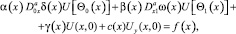
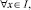(3)

где 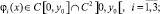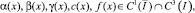причем 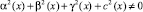a – вещественное число, 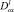, 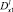– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования.

Пусть U(x, 0) = τ(x); Uy(x, 0) = ν(x). Решение задачи Коши в области Ω– имеет вид [5]

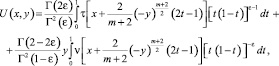
где 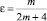, Γ(z) – гамма функция Эйлера.

Учитывая значения Θ0(x) и Θ1(x) в последнем равенстве, получим

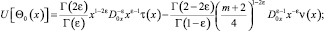
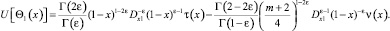
Имеет место

Теорема. В области Ω существует единственное решение задачи (1)–(3), если выполняются условия

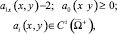(4)

и либо a = ε; 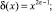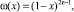(5)

и выполняются условия

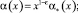
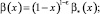
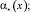
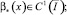
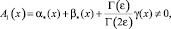
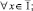(6)

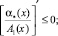
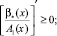
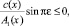
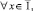(7)

либо a = 1 – ε; δ(x) = ω(x) = 1, (8)

и выполняются условия

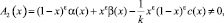
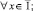(9)

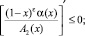
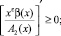
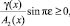
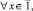(10)

где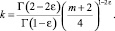

Доказательство. Пусть выполняются условия (5). Тогда, подставляя найденные значения U[Θ0(x)], U[Θ1(x)] в краевое условие (3), найдем

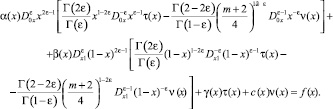
Откуда, с учетом того, что 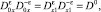где D0 – единичный оператор, получим

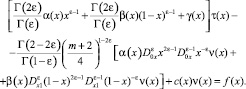(11)

Преобразуем двойные интегралы, входящие в выражение (11) [4]:

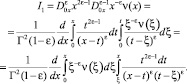
Проделав некоторые преобразования, получим

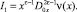(12)

Аналогичным образом получаем

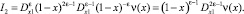(13)

С учетом (12) и (13) уравнение (11) принимает вид

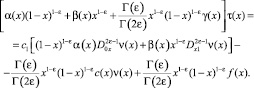(14)

С учетом выполнения условия (6) перепишем (14) в виде

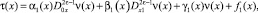(15)

где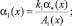

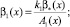
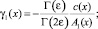
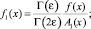
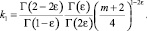
Выражение (15) является основным функциональным соотношением между функциями τ(x) и ν(x), принесенным на линию y = 0 из области Ω–.

Докажем, что решение задачи (1)–(3) единственно при выполнении условий (4)–(7) теоремы. При f(x) = 0, с учетом равенства (15), получаем

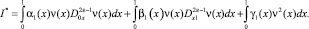
Проделав некоторые преобразования, заключаем, что I* ≥ 0.

С другой стороны, переходя в уравнении (1) к пределу при y → +0, получаем

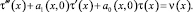(16)

Умножая последнее на τ(x), а затем интегрируя от 0 до 1, с учетом однородных граничных условий, получим

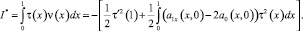(17)

Учитывая условие 4, имеем I* ≤ 0. Следовательно I* = 0.

Следовательно, ν(ξ) = 0 почти всюду, а так как ν(x) непрерывна по условию, то ν(ξ) = 0 всюду. Отсюда видно, что ν(x) = 0 и при f(x) = 0 следует, что τ(x) = 0.

Таким образом, U(x, y) º 0 в Ω– как решение задачи Коши с нулевыми данными, а в Ω+ как решение задачи (1), τ(x) = 0, U(0, y) = 0; U(1, y) = 0; Ux(0, y) = 0 [1–3]. Отсюда заключаем, что решение задачи (1)–(3) при выполнении условий (4)–(7) единственно.

Для доказательства существования решения задачи рассмотрим уравнение (1) в области Ω+. Получаем задачу (16)

τ(0) = φ1(0); τ(1) = φ2(0); τ′(0) = φ3(0). (18)

Пусть a1(x, 0) = s1; a0(x, 0) = s0; s1, s0 = const ≠ 0. Делая замену неизвестной функции τ(x) в равенстве (16) по формуле

τ(x) = z(x) + g(x), (19)

где

,

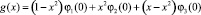и учитывая граничные условия, получим относительно функции τ(x) задачу

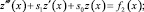(20)

z(0) = 0; z(1) = 0; z′(0) = 0, (21)

где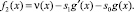

Решение задачи (20), (21) относительно τ(x) существенно зависит от корней характеристического уравнения k3 + s1k + s0 = 0. Введем обозначение

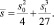
Рассмотрим случай, когда 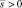. В этом случае общее решение (16), (18) можно записать в виде

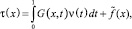(22)

где G(x, t) – функция Грина однородной задачи, 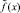– функция, выраженная через заданные.

С учетом выполнения условий (4)–(7) теоремы исключим τ(x) из (22) и (15). Учитывая условия (6), получим

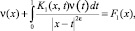(23)

где K1(x, t) и F1(x) – функции, выраженные через известные, заданные функции.

При γ1(x) ≠ 0 или, что то же самое c(x) ≠ 0, уравнение (23) есть уравнение Фредгольма второго рода со слабой особенностью в ядре и непрерывной правой частью, безусловная разрешимость которого заключается из единственности решения задачи.

По найденному ν(x) из (15) определяется τ(x), а решение задачи (1)–(3) в области Ω– как решение задачи Коши, а в области Ω+ решение задачи 1 определяется по формуле [5]

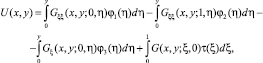
где G(x, y, ξ, η) – функция Грина задачи (1), (2), U(x, 0) = τ(x).

Аналогичным образом рассматриваются случаи когда 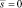и когда .

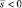Пусть a1(x, 0), a0(x, 0) ≠ const. В этом случае поставленная задача, аналогично предыдущему случаю, сводится к интегральному уравнению Фредгольма второго рода относительно функции ν(x), со слабой особенностью в ядре и непрерывной правой частью, вида

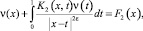
где K2(x, t) и F2(x) функции, выраженные через известные, заданные функции.

Доказательство единственности и существования решения поставленной задачи при выполнении условий (8)–(10) теоремы проводится аналогично.

Рецензенты:

Хачев М.М., д.ф.-м.н., профессор, зав. кафедрой высшей математики, ФГБОУ ВПО «Кабардино-Балкарский государственный аграрный университет им. В.М. Кокова, г. Нальчик;

Аджиев А.Х., д.ф.-м.н., профессор, зав. отделом стихийных явлений, ФГБУ «Волжский гуманитарный институт», г. Волжский.

Библиографическая ссылка