Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Вахитов Ш.Я. 1 Башарин С.А. 1 Смирнова Н.А. 1 Щитов И.Н. 1

---

1 ФГОУ ВО «Санкт-Петербургский государственный институт кино и телевидения»

В статье рассмотрена распределенная колебательная система в виде защемленной по краю круглой пластины с жесткой центральной частью. Такие колебательные системы часто встречаются в виде диафрагм в электроакустической аппаратуре, например в электродинамических преобразователях купольного типа, а также подобные им в приборостроении и машиностроении. Предложен способ замещения такой пластины простой колебательной системой с сосредоточенными параметрами. Получены аналитические соотношения для расчета величины эквивалентной гибкости и эквивалентной площади гофра и диафрагмы в целом. Показано, что ранее предложенные формулы не приемлемы для расчета этих параметров в некоторых динамических преобразователях, т.к., во-первых, не согласуются с классическими представлениями о колебаниях пластин, во-вторых, противоречат данным многочисленных экспериментов. Полученные аналитические модели создают теоретическую базу для расчета и дальнейшей разработки целого ряда приборов и устройств.

Статья в формате PDF

817 KB

аналитическая модель

колебательная система

динамический преобразователь

1. Андреева Л.Е. Упругие элементы приборов. – М.: Машиностроение, 1981. – 392 с.

2. Вахитов Ш.Я. Современные микрофоны. Теория, проектирование. – СПб.: Изд. СПбГУКиТ, 2003. – 396 с.

3. Вахитов Я.Ш. Теоретические основы электроакустики и электроакустическая аппаратура. – М.: Искусство, 1982. – 415 с.

4. Гутин Л.Я. Избранные труды. – Л.: Судостроение, 1977. – 600 с.

5. Лэмб Г. Динамическая теория звука. – М.: Госиздат физмат литературы, 1960. – 372 с.

6. Стретт (Рэлей) Д.В. Теория звука, т.1. – М.: Госиздат технико-теоретической литературы, 1955. – 504 с.

7. Тюрин А.М., Сташкевич А.П., Таранов Э.С. Основы гидроакустики. – Л.: Судостроение, 1966. – 296 с.

Простейшие колебательные системы, параметры которых (масса, упругость, трение) могут быть пространственно обособлены друг от друга, принято называть системами с сосредоточенными параметрами. Однако в реальных колебательных системах часто оказывается, что элементы массы, гибкости и трения пространственно не разделимы, поэтому их называют системами с распределенными параметрами, или просто распределенными системами. Классическими примерами таких систем являются струна, стержень (одномерные); мембрана, пластина (двумерные). Внешне трудно отличить струну от стержня, а мембрану от пластины. Однако в характере их колебаний имеется существенная разница, обусловленная природой их упругой реакции: в струне и мембране эти силы возникают в результате достаточно сильного внешнего натяжения, в стержне и пластине – как результат их собственной жесткости. Так как всякая реальная система обладает конечной толщиной, а значит, и определенной собственной жесткостью, отнесение распределенной системы к тому или иному типу зависит от характера преобладающих упругих сил.

В этом случае каждый колебательный элемент можно рассматривать как простую колебательную систему (с одной эквивалентной массой, гибкостью и трением), резонансная частота которой практически совпадает с первой собственной частотой замещаемой распределенной системы. К такому замещению обычно прибегают для упрощения расчетов электроакустических аппаратов, имеющих сложную акустико-механическую систему. Как правило, применяют энергетический метод нахождения эквивалентных параметров, впервые предложенный еще Рэлеем [6], подробнее с которым можно познакомиться в отечественной литературе, например в работе [3]. Здесь мы отметим только, что основными критериями эквивалентности в этом методе являются:

– сохранение величины кинетической (E_к), потенциальной (E_n) и диссипативной (E_q) энергии (последнее в целом ряде случаев не является столь существенным), что позволяет определить соответственно эквивалентную массу (m_э), гибкость (с_э) и активное сопротивление (r_э);

– сохранение величины, распределения и характера работы внешних сил, что позволяет определить эквивалентные размеры и эквивалентное колебательное смещение замещающей системы (а значит, скорость и ускорение).

Любой электроакустический аппарат рассчитывается для работы в некотором диапазоне частот, поэтому, как правило, конструкцию аппарата выбирают такой, чтобы ее упругие элементы обладали не более чем одной собственной частотой (< f₀₁) в заданном диапазоне, но в ряде случаев, например в электроакустической аппаратуре при симметрии колебательной системы, вполне реально, что устройство работает, как простая колебательная система и в диапазоне до второй симметричной моды [2], величину которой можно вычислить по приближенной формуле

,

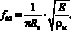где Е и ρ_м – модуль упругости [н/ м²] и плотность материала упругого элемента; R_к – радиус кривизны купола (рис. 1).

Во избежание потери в номинальном диапазоне частот поршневого характера колебаний купола диафрагмы (рис. 1) величина f₀₂ и соотношение радиусов кривизны купола и гофра должны удовлетворять системе неравенств

.

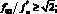
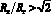Задачей настоящей работы является определение эквивалентных параметров подвижного узла динамических катушечных преобразователей купольного типа (рис. 1). Подобные подвижные системы широко используют в электроакустической аппаратуре (динамических микрофонах, головных телефонах, высокочастотных громкоговорителях прямого излучения, в рупорных громкоговорителях), похожие узлы встречаются в некоторых гидроакустических преобразователях, а также в упругих элементах других приборов и ряде устройств машиностроения [1, 7].

О вычислении полной эквивалентной массы подвижной системы

Отметим здесь, что вычисление эквивалентной массы таких преобразователей, как правило, не вызывает больших трудностей. Полную эквивалентную массу подвижной системы, можно вычислить [2] по следующей формуле:

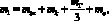(1)

где массу звуковой катушки можно найти по формуле

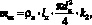(2)

где ρ_п – плотность материала провода; l_п – его длина и d_п – диаметр, k₂ – технологический коэффициент, учитывающий массу изоляции провода и клеевого слоя, а также массу каркаса звуковой катушки (как правило, имеющего место только в случае излучателя звука). Его величина обычно лежит в пределах k₂ ≈ 1,2–1,4.

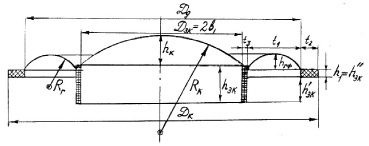
Рис. 1. Пример колебательной системы динамического катушечного преобразователя

Отметим, что толщину купола Δк часто, для большей жесткости, приходится делать больше, чем толщину гофра ΔГ. Это выполняется или путем присоединения к куполу дополнительных слоев материала, или раздельной прессовки купола и гофра диафрагмы, массу которых можно найти по формулам

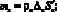
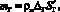(3)

где 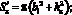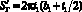– площади купола и гофра.

Соколеблющуюся массу воздуха можно определить по известной формуле

,

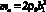где плотность воздуха ρ₀ = 1,23 кг/м³. Отметим, что масса звуковой катушки (2) обычно составляет в полной массе такой подвижной системы (1) около 70–90 %, поэтому даже в случае некоторых погрешностей при вычислении остальных составляющих полной массы обычно получаются в итоге весьма достоверные результаты. Резонансная частота ПС определяется по известной формуле

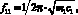
где с₁ – эквивалентная гибкость диафрагмы. С её расчетом в подобных системах и возникают обычно сложности.

Как станет ясно из следующего раздела статьи, ни одно из предложенных ранее аналитических соотношений не позволяет с должной степенью точности рассчитать эквивалентную гибкость подобных диафрагм, что, в свою очередь, делает невозможным расчетное проектирование выше указанных видов современной аппаратуры. В нахождении адекватной формулы расчета эквивалентных гибкости и площади таких колебательных систем и состоит актуальность данной работы.

Определение эквивалентной гибкости и действующей площади диафрагмы

Впервые аналитическое соотношение для расчета упругости подвеса (воротника, гофра) диафрагмы динамического микрофона S_вр (рис. 2) было предложено Л.Я. Гутиным [4]. В принятых в нашей работе обозначениях (рис. 1, 2) это выражение для гибкости с_вр принимает вид

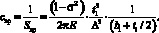(4)

При проектировании целого ряда моделей динамических микрофонов, а также при расчете головок (преобразователей) рупорных громкоговорителей нами было замечено, что результаты расчета по формуле (4) имеют весьма существенное (приблизительно в 5–6 раз) расхождение с экспериментом в сторону увеличения гибкости. Полагая, что подобное несоответствие обусловлено заменой в [4] гофрированной диафрагмы с жестким куполом моделью пластины с жесткой центральной частью, мы сделали попытку применить при расчете с_вр формулу, приведенную в [1] для металлических гофрированных мембран толщиной порядка 0,2–2 мм с многошаговой глубокой гофрировкой. Однако и эта попытка не дала положительных результатов, т.к. расхождения с экспериментом расчета по этим формулам были еще большими, но уже в сторону занижения коэффициента гибкости с_вр.

В конструкциях диафрагм динамических преобразователей с «полушаговой» гофрировкой такое предположение, на наш взгляд, является неоправданным, и диафрагму следует рассматривать не как мембрану, а как неоднородную пластину с жестким центром. В силу этих причин мы сочли целесообразным провести собственный вывод расчетного соотношения для с_вр, результаты которого приведены в данной статье.

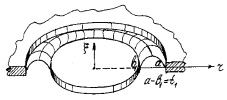
Рис. 2. Физическая модель колебательной системы с жесткой центральной частью, закрепленной по периметру. Здесь ∆ – толщина упругого элемента [м]; Е и σ – модуль упругости [н/м²] и коэффициент Пуассона материала упругого элемента; а – внешний радиус закрепления [м]; b – радиус жёсткой части [м]; t = а – b [м]; γ = b/a

Известным способом замещения распределенных систем эквивалентными с сосредоточенными параметрами [3, 5] найдем эквивалентную гибкость круглой однородной пластины радиуса а и толщиной D. Смещение точек такой пластины на частотах, не превышающих первого собственного резонанса пластины (т.е. f < f₀₁), выражается функцией

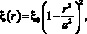(5)

где ξ₀ – амплитуда смещения центра закрепленной по краю круглой пластины, r – радиус точки поверхности.

Считая, что площадь эквивалентного поршня S_э = πа², путем интегрирования этого выражения найдем объем вытесняемого пластиной воздуха V₁ = ξ₀·πa²/3 и величина ее эквивалентного смещения ξ_э

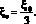(6)

Согласно [6, 5] потенциальную энергию пластины в принятых нами обозначениях можно выразить как

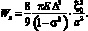(7)

В замещающей эквивалентной системе потенциальная энергия 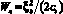, а величина xэ определяется выражением (6). Приравняв энергии реальной и эквивалентной систем, после алгебраических преобразований получим

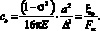(8)

Для гибкости, определяемой относительно центра пластины со смещением ξ₀, в соответствии с [1, 5] получим

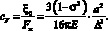(9)

Очевидно, что формула Гутина при ее корректности в пределе (при b₁ → 0, t₁ → а) в зависимости от площади приложения силы (центральная точка или равномерно распределенная по площади) и используемого смещения (ξ₀ или ξ_э) должна принимать вид либо (8), либо (9). Однако в указанных пределах она (4) преобразуется к виду

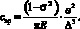(10)

Из сравнения формул (8)–(10) очевидно, что величина с_вр для однородной круглой пластины отличается соответственно в 16 и 16/3 раза. Это указывает на ошибочность полученного Гутиным аналитического выражения и, как следствие, неприменимости его для расчета гибкости диафрагм.

На основе описанной методики определим коэффициент гибкости «воротника», образованного периферийной частью пластины радиуса а, центральную часть которой занимает жесткий диск радиуса b (рис. 3, б), имеющий по всей площади одинаковое смещение ξ_в. Следовательно, в отличие от однородной пластины (рис. 3, а), переменное смещение ξ_(r) реализуется на ширине «воротника» t = a – b. А при b, стремящемся к 0, модель (б) должна стремиться к модели (а).

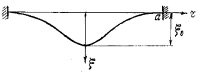
а

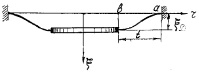
б

Рис. 3. Характер колебаний круглой пластины, однородной (а) и с жестким центром (б), под действием приложенной внешней силы

Обозначив переменный радиус элементарного кольца как r, можем выразить закон смещения ξ(r) по аналогии с соотношением (5), как

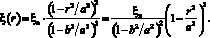(11)

Это соотношение удовлетворяет граничным условиям

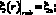
Очевидно, что при равенстве воздействия величина смещения жесткой центральной части ξ_в будет меньше смещения центра ξ₀ равновеликой однородной пластины, что зависит не только от упругих характеристик участка, лежащего в пределах b < r < a, но и от радиусов защемления этого участка. Величину ξв возможно определить, произведя процедуру нахождения эквивалентной гибкости однородной пластины радиусом t = a – b, аналогичную ранее проделанной (см. выражения (5)–(9)). В результате получим

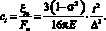(12)

Откуда, взяв отношение (12) к (9), найдем относительное смещение центров таких пластин при р = const, т.е.

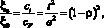(13)

где r = b/a.

Учитывая изложенное, определим величину вытесняемого объема воздуха V₂ как

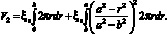(14)

Производя интегрирование и алгебраические преобразования с учетом (13), получим

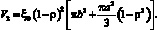(15)

Разделив полученное выражение на общую площадь пластины S₂ = πa², найдем среднее по площади такой пластины смещение xэр:

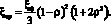(16)

Приравнивая потенциальные энергии исследуемой пластины и равновеликой однородной [6, 5], имеем

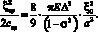
Откуда, после подстановки (16) и алгебраических преобразований определим величину гибкости пластины с жестким центром

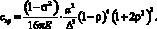(17)

Или в более удобном для расчетов виде:

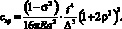(18)

Разделив величину вытесняемого пластиной объема воздуха (15) на смещение его центральной части (купола) (13), получим выражение для площади эквивалентного поршня:

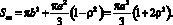(19)

Здесь первое слагаемое – площадь купола, второе – эквивалентная площадь гофра (подвеса). Действительная площадь гофра

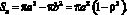
Очевидно, что соотношение эквивалентной и действительной (физической) площадей гофра

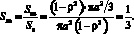
Далее была осуществлена проверка полученных в работе формул путем сопоставления данных эксперимента и расчета по конечным формулам (18), (19), а также массы по (1)–(3). После чего рассчитывалась частота механического резонанса подвижной системы нескольких моделей динамических преобразователей (микрофонов, купольных головок громкоговорителей). Затем, в соответствии с действующими стандартами (ГОСТ Р53575-2009 и ГОСТ Р53576-2009) проводились измерения этих резонансных частот на нескольких образцах преобразователей. Расхождение расчетных и экспериментальных результатов составляло не более 10 %, что, как правило, даже меньше допустимого разброса по этому параметру изделий из одной партии.

Выводы

Разработан ряд вопросов теории колебательных систем динамических катушечных купольных преобразователей, таких как определение эквивалентной гибкости и эквивалентной площади диафрагмы в целом и подвеса (гофра). Показано, что соотношение, ранее полученное Гутиным, неприемлемо для практики расчета таких преобразователей, т.к., во-первых, не согласуется с классическими представлениями о колебаниях однородных пластин, во-вторых, противоречит данным экспериментов.

В отличие от формулы Гутина, полученные нами выражения для гибкости пластины с жестким центром приводятся к (при ρ → 0) к классическим выражениям для гибкости однородной пластины. Таким образом, последние являются частным случаем от полученных нами более общих выражений. Полученные в работе аналитические модели и расчетные соотношения позволяют создать теоретическую базу для разработки методов проектирования различных типов купольных и ряда других преобразователей.

Рецензенты:

Майзель А.Б., д.т.н., профессор, начальник отдела, ОАО «ЦКБ МТ «Рубин», г. Санкт-Петербург;

Уваров В.К., д.т.н., профессор, ФГБОУ ВО «Санкт-Петербургский государственный институт кино и телевидения», г. Санкт-Петербург.

Библиографическая ссылка