Общая идея спонтанной утраты жизнеспособности, положенная в основу формулы Б. Гомпертцем [4], является и в настоящее время краеугольным камнем современной геронтологии, так как позволяет наиболее просто и точно описывать возрастное изменение смертности человека и, видимо, других организмов. Б. Гомпертц рассматривал смертность как величину, обратную жизнеспособности – способности противостоять всей совокупности разрушительных процессов. Он предположил, что жизнеспособность снижается с возрастом пропорционально ей самой в каждый момент. Такое неспецифическое повышение с возрастом уязвимости организма ко всем воздействиям и носит название старения как такового.
Модель, разработанную Б. Гомпертцем и впоследствии дополненную Мейкхамом [5], можно условно отнести к классу механистических моделей, поскольку она основана на предположении об износе в терминах идеализированной так называемой «жизнеспособности». Уровень этой абстрактной (кумулятивной для организма) величины обозначен X(t), при t ≥ 0, где 0 – момент появления (в т.ч. рождения) особи с начальным уровнем X(0) = x (с x > 0). В модели Гомпертца предполагается, что уровень жизнеспособности «изнашивается» с некоторой постоянной интенсивностью α ≥ 0:
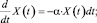X(0) = x. (1)
Решением уравнения (1) является
X(t) = x∙exp{–α∙t}, (2)
а смертность μH(t) в модели Гомпертца предполагалась обратно пропорциональной величине жизнеспособности:
μH(t) = x–1∙exp{α∙t}. (3)
Эта формула была впоследствии модифицирована У. Мейкхамом, добавившим в формулу Б. Гомпертца постоянный коэффициент R > 0, представляющий не зависящую от возраста компоненту смертности. Этот коэффициент имеет экологическую, социальную или экономическую природу и заметно изменяется в ходе эволюции человечества. Постоянную R принято называть параметром давления среды. При этом уровень смертности в такой составной модели Гомпертца – Мейкхама равен
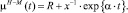(4)
Заметим, что модель Гомпертца – Мейкхама не отвечает наблюдаемому явлению многостадийности старения. В частности, она не учитывает явлений онтогенетических перестроек в некоторые моменты времени τ0, τ1, τ2, ... с τ0 = 0 и τn < τn+1 для всех n = 0, 1, 2, .... После каждого из таких моментов τn наблюдается период повышенной смертности. Это локальное увеличение смертности вызвано возмущениями, привнесенными метаболической перестройкой при смене стадий. Оно влечет для живых систем последующую локальную дополнительную адаптацию. Так, для τ0 = 0 это увеличение смертности соответствует повышенной детской смертности, для начала периода фертильности – пик юношеской смертности, для момента наступления климактерической паузы (или андропаузы) – соответствующий им подъем смертности [3].
Материалы и методы исследования
Настоящий раздел работы посвящен построению математической модели, частично объясняющей закономерность возникновения стадий процесса старения. Основным предположением, положенным здесь в основу модели наблюдаемого феномена смены онтогенетических фаз и уровней стабильного метаболизма, является следующая гипотеза. Мы предполагаем, что для компенсации метаболической недостаточности (возникающей в результате исчерпания ресурсов текущей стадии) реализуется компенсаторная глобальная адаптивная перестройка, обеспечивающая на последующей стадии полноценное функционирование в рамках новой стадии. То есть предполагается, что метаболические перестройки не могут проводиться ни постоянно, ни слишком часто, поскольку каждая из них влечет временную локальную дезадаптацию, временное увеличение уязвимости и повышение смертности.
Таким образом, каждая структурная перестройка должна обеспечить возможность системе устойчиво функционировать, как можно дольше «обходясь» без очередного изменения структуры. В терминах модели это можно сформулировать следующим образом.
Решается задача об оптимизации выбора моментов смены стадий в форме нахождения компромисса: за каждую смену стадий приходится «платить» временным увеличением смертности, обусловленным локальной дезадаптацией. При этом каждая такая смена стадий обуславливает возникновение нового устойчивого режима функционирования, устраняя дезадаптацию, сформировавшуюся в результате накопившегося износа, старения.
В качестве адаптивной перестройки при отдельных сменах стадий встречается перевод системы в режим «форсированной» выработки энергии, что приводит к соответствию уровня производимой в единицу времени энергии (т.е. мощности) уровню необходимых затрат. В качестве альтернативы может наблюдаться изменение поведения, приводящее к существенному снижению ресурсных затрат, что также приводит к соответствию, адаптации.
Таким образом, представляется интересным рассмотреть в качестве основного процесс уровня соответствия A = (A(t))t≥0 (accordance) со значением A(t) в каждый момент времени t ≥ 0, равным
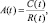(5)
где C(t) – мощность (capacity), которую потенциально может выработать субъект износа (приведенная, нормированная – например, на единицу веса); R(t) – приведенная мощность, которая в среднем требуется (requirements) при его усредненной нагрузке (интенсивности эксплуатации, образе жизни, поведении).
В приведенных предположениях для наблюдаемой стадийности онтогенетических процессов моменты смены стадий обозначают τ0, τ1, τ2, ... с τ0 = 0 и τn < τn+1 для всех n = 0, 1, 2, ... Тогда на каждом интервале времени t ∈ [τn, τn+1) при n = 0, 1, 2, ... предполагается стабильность в выполнении соотношения Гомпертца
dA(t) = –αn∙A(t)dt, (6)
т.е. постоянное при t ∈ [τn, τn+1) значение параметра αn.
При этом критерием сохранения стадии является при t ∈ [τn, τn+1) для каждого n = 0, 1, 2, ... соотношение
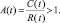(7)
В случае A(t) ≤ 1 возникает состояние дезадаптации, приводящее к смене стадий (адаптивной, следовательно). Таким образом, оказывается возможным рекуррентно определить в общем случае, не обязательно отвечающем только соотношению (6), моменты смены стадий: τ0 = 0, и при каждом n = 0, 1, 2, ...
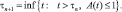(8)
Для усредненной оценки в первом приближении допустимо соотношение (6) с решением при каждом n = 0, 1, 2, ... для t ∈ [τn, τn+1) уравнения
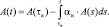(9)
Результаты исследования и их обсуждение
Рассмотрим первую стадию при t ∈ [τ0, τ1) = [0, τ1) и сформулируем задачу оптимального выбора продолжительности стадии. В рамках модели, описанной выше, в соответствии с формулой (9) справедливо
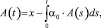(10)
где A(0) = x и α0 = α∙x + μ, где параметр α > 0 определяет уровень зависимости износа от базовой мощности, а параметр μ ≥ 0 позволяет учитывать независящие от базовых энергетических уровней процессы разрушения (например, структурные, давление среды и другие)
Тогда при t ∈ [0, τ1)
A(t) = x∙e–αxt∙e–μt. (11)
Здесь соотношение α0 = α∙x + μ допустимо в рамках предположения о том, что ресурсы адаптации исчерпываются со скоростью, пропорциональной выбранной базовой мощности C(0) (т.е. базового для данной стадии уровня энергопродуктивности), и присутствует постоянное независимое воздействие на организм. Это предположение восходит, в частности, к свободнорадикальной теории старения (уровень свободных радикалов пропорционален базовой энергопродуктивности) и генетической теории старения (частота повреждений ДНК пропорциональна уровню экспрессии, которая, в свою очередь, пропорциональна базовому уровню метаболизма).
В соответствии с (8) смена стадий происходит в момент времени T = T(x) при выполнении равенства
A(t) = x∙e–αxT∙e–μT = 1. (12)
В рассматриваемом случае равенство (12) означает, что τ1 = T = T(x).
Возникает задача выбора оптимальной величины x, доставляющей максимум продолжительности стадии T = T(x):
= T(x) → max, x > 1. (13)
Решением задачи оптимизации (12) приводит к соотношению eαxT+μT = x, произведя преобразования, получаем lnx = lneαxT+μT или lnx = T(x)∙(αx + μ) и, таким образом, выполняется базовое равенство, устанавливающее явную зависимость T(x):
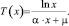(14)
Экстремум (максимум) достигается при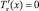 
, что определяет вид «оптимальной» зависимости T = T(x).
Вычислим
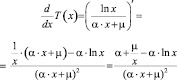(15)
приводят к соотношению:
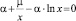(16)
или
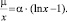(17)
Уравнение (17) имеет единственное решение x* ≥ e.
Утверждение. В предположениях (10)–(17) глобальный максимум функции Т(х) достигается в точке x*, где x* – решение уравнения (17).
Заметим, что уравнение (17) не имеет явного решения, но с требуемой точностью может быть вычислено численно. Таким образом, «оптимальная» величина начального (базового) уровня x стабильной стадии равна x*, которое вычисляется из уравнения (17).
Продифференцируем обе части уравнения (12):
(x∙e–αxT∙e–μT)′ = 0. (18)
Рассмотрим левую часть уравнения (18):
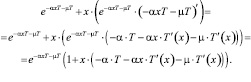
Таким образом, получаем
1 + x∙(–α∙T – α∙x∙T′(x) – μ∙T′(x)) = 0; (19)
x∙(α∙T + α∙x∙T′(x) + μ∙T′(x)) = 1. (20)
«Оптимальная» величина начального (базового) уровня x стабильной стадии равна x*, тогда из уравнения (20) получаем
x*∙(α∙T + α∙x*∙T′(x*) + μ∙T′(x*)) = 1, (21)
но T′(x*) = 0, тогда
x*∙α∙T = 1. (22)
Соответственно, получаем, что величина максимальной продолжительности (стабильной) стадии T определяется из (22) и зависит от x*.
Теорема. В предположениях (10)–(23) вид функции T*(x) определяется соотношением
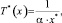(23)
где x* – решение уравнения (17).
Доказательство. Формальное доказательство теоремы очевидно вытекает из (22) и описания математической модели.
Выводы
Полученные таким образом величины {x*, T*} инвариантны к номеру стадии, следовательно, они могут в первом приближении рассматриваться в качестве единообразных для всего процесса старения, определяющими его многостадийность. Настоящее приближение является демонстрационным, допускает легкие обобщения и может служить основой для первичного построения моделей многостадийного старения.
Учет многостадийности и репаративных процессов допустим и в рамках механистической модели износа, обобщающей модель Гомпертца – Мейкхама на случай многих стадий. При этом адекватными становятся объяснения эпизодических популяционных повышений смертности при смене стадий старения. Также допустимо рассмотрение оптимизационных задач при определении величин уровней метаболизма и продолжительности стадий.
Рецензенты:
Седова Н.О., д.ф.-м.н., профессор, Ульяновский государственный университет, г. Ульяновск;
Мищенко С.П., д.ф.-м.н., профессор, Ульяновский государственный университет, г. Ульяновск.
Библиографическая ссылка
Бутов А.А., Шабалин А.С., Коваленко А.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МНОГОСТАДИЙНОГО СТАРЕНИЯ АДАПТИВНЫХ СИСТЕМ // Фундаментальные исследования. – 2015. – № 9-2. – С. 219-222;URL: https://fundamental-research.ru/ru/article/view?id=39077 (дата обращения: 26.04.2024).