В задачах качественного анализа и обработки данных слабо формализованные объекты используются при моделировании разнообразных динамических процессов. Модели такого рода, прежде всего, предназначены для мониторинга состояния и оптимального управления неструктурированными или слабо структурированными процессами, текущее знание о которых недостаточно [1, 2, 11 и др.].
Любому слабо формализованному объекту присущи следующие характеристики:
- качественная природа многих параметров описания объекта;
- неоднородность (разнотипность) шкал, применяемых для измерения параметров;
- нелинейность взаимосвязей используемых характеристик объекта;
- многоуровневая иерархическая организация взаимосвязи составляющих объекта, часто с нечеткими отношениями между ними;
- многообразие возможных форм взаимодействия составляющих объекта, порождающее неоднородность поступающей информации;
- многокритериальность оценивания состояния объекта, причем нередко – несогласованность, противоречивость критериев [11].
В литературе имеются модели конкретных слабо формализованных объектов и частные задачи распознавания их структуры. Однако не сформирована концептуальная модель, адекватно представляющая слабо формализованный объект и обеспечивающая задачу распознавания образа этой структуры. Цель данного исследования – разработка концептуальной модели слабо формализованного объекта для общей задачи распознавания образа его структуры при диагностике и оценке состояния такого объекта.
Известно, что задача распознавания образа заключается в том, чтобы, используя исходные данные, отнести рассматриваемый объект к определенному классу. Формальная постановка такой задачи выглядит следующим образом [4].
Задано множество объектов, относительно которых выполняется классификация. Данное множество представлено подмножествами – классами. Известно описание всего множества и характеристика классов. Имеется информация о некотором объекте. Требуется установить, к какому классу можно отнести этот объект.
Как правило, решение задачи распознавания образа содержит два этапа. На первом этапе осуществляется предобработка данных об объекте, подлежащем распознаванию (выделяются характерные признаки, определяются значения главных факторов и т.п.). На втором этапе с помощью функции принятия решения (решающей функции) получают искомый ответ о принадлежности объекта к определенному классу. Ясно, что полученное решение имеет вероятностный характер.
Слабо формализованные объекты являются сложными системами, в которых человек играет активную роль. При их моделировании необходимо учитывать следующие условия.
Во-первых, для получения адекватных выводов о рассматриваемой системе не следует стремиться к точным и строгим методам, которые пригодны для сравнительно простых объектов. Нужно использовать приближенные подходы, реализуемые на основе лингвистических переменных, которые соответствуют неточному (нечеткому) отражению человеком окружающего мира [6].
Во-вторых, необходимо расширить привычные возможности информационного обеспечения модели слабо формализованного объекта за счет обширного информационного потенциала знаний о рассматриваемых процессах в виде неформализованных первичных мнений, представлений, оценок реальных людей, вовлеченных в эти процессы. Оптимальное использование указанных «залежей» первичной информации будет реализовано, если ее носители «включатся» в проводимое исследование как его субъекты [3]. При этом целенаправленное использование информационного потенциала всех субъектов исследования существенно «обогатит» создаваемую концептуальную модель [8].
Практически любой слабо формализованный объект можно представить концептуальной моделью с трехуровневой иерархической структурой [8, 10]. Это значит, что для формирования модели, обеспечивающей диагностику состояния конкретного объекта С, нужно определить макроуровень данного объекта (уровень макрокомпонентов {Pj}) и операциональный уровень (уровень проявлений {xr}.
Таким образом, общая задача распознавания структуры слабо формализованного объекта C состоит из следующих подзадач:
1) комплексной подзадачи распознавания макроструктуры объекта {Pj};
2) комплексной подзадачи распознавания операциональной структуры объекта {xr}.
В теории искусственного интеллекта, говоря о распознавании образа конкретного объекта, имеют в виду процедуру его соотнесения с тем или иным классом [5, 7, 9] и др. Возможность разрешения такой задачи означает:
- предварительное разбиение множества всех объектов на совокупность непересекающихся подмножеств (классов) с конкретизацией признаков, отличающих объекты одного класса от объектов других классов;
- определение значений тех признаков, которые характеризуют каждый из классов, по массиву всей информации, доступной для измерения;
- применение правил принятия решения об отнесении рассматриваемого объекта к конкретному классу по значениям характерных признаков этого объекта;
- оценивание достижимого качества, которое характеризует полученное решение задачи распознавания образа конкретного объекта.
Ясно, что формализованное решение задачи распознавания образа того или иного объекта обеспечивается только на основе совокупности признаков, наиболее существенных для того, чтобы достаточно полно описать и конкретизировать образ объекта [9]. Именно для такого описания необходима соответствующая модель объекта.
Опираясь на традиционный смысл задачи распознавания [7], формирование каждого из уровней объекта C можно реализовать как процесс решения соответствующих задач классификации:
а) классификация макрокомпонентов объекта;
б) классификация проявлений объекта. При этом необходимо рассмотреть две обеспечивающие задачи:
- формирование исходной совокупности макрокомпонентов (проявлений) для первой (второй) комплексной подзадачи;
- определение оптимальной совокупности макрокомпонентов (проявлений) для первой (второй) комплексной подзадачи (рисунок).
Охарактеризуем каждую из подзадач, представленных на рисунке.
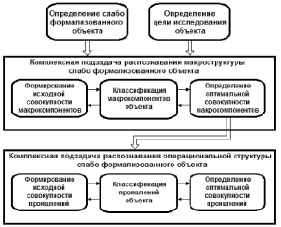
Модель задачи распознавания структуры слабо формализованного объекта
I. Комплексная подзадача распознавания макроструктуры объекта
Обеспечивающая задача «Формирование исходной совокупности макрокомпонентов» формирует макроструктуру объекта в виде совокупности макрокомпонентов {Pj}, описывающих смысловое содержание рассматриваемого объекта (пространство образов). В силу неполноты информации об объекте C совокупность исходных макрокомпонентов не может быть закрытой, имеющей наперед заданное количество составляющих. Поэтому при необходимости может быть решена дополнительная задача распознавания, позволяющая отобрать макрокомпоненты, минимально необходимые для диагностики состояния объекта.
Каждый макрокомпонент может быть представлен своим описанием I(Pj) в полном пространстве выделенных признаков Y = {yi}, i = 1, 2, ..., n, с помощью которых макрокомпонент Pj характеризуется с позиции наблюдателя:
I(Pj) = (y1(Pj), y2(Pj), y3(Pj), …, yn(Pj)).
В простейшем случае такое описание может содержать следующие два значения:
- макрокомпонент Pj не обладает i-м признаком yi = 0;
- макрокомпонент Pj обладает i-м признаком yi = 1.
Формируется три класса макрокомпонентов: P – макрокомпоненты, принадлежащие объекту C; 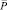 – макрокомпоненты, не принадлежащие объекту C; P0 – неопределенный класс. Тогда задача распознания макроструктуры заключается в отнесении каждого Pj к одному из выделенных классов
– макрокомпоненты, не принадлежащие объекту C; P0 – неопределенный класс. Тогда задача распознания макроструктуры заключается в отнесении каждого Pj к одному из выделенных классов 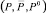 на основе его описания I(Pj).
на основе его описания I(Pj).
Решение об отнесении принимается на основе решающей функции, содержащей правила отнесения макрокомпонента Pj к тому или иному классу. Если использовать пороговую решающую функцию, то количество признаков, которыми обладает макрокомпонент, должно быть не меньше 50 % от общего числа признаков (значение порога в каждой конкретной задаче устанавливается экспертным путем).
Уровень макрокомпонентов может включать в себя несколько подуровней. Это означает, что макрокомпоненты Pj могут быть представлены составляющими {Plj}, соответствующими конкретным процессам, протекающим в рассматриваемом объекте.
В силу неоднозначности имеющейся информации об объекте C структура его макрокомпонентов не может быть четко определенной. Поэтому дальнейшее распознавание макроструктуры объекта реализуется путем классификации его макрокомпонентов, которая основана на проведении анализа «снизу – вверх». В результате определяется место каждой составляющей Plj в пространстве выделенных классов (макрокомпонентов Pj).
Аналогично макрокомпонентам каждая составляющая Pjl может быть представлена своим описанием в пространстве выделенных признаков Y, с помощью которых макрокомпонент Pjl характеризуется с позиции наблюдателя:
I(Pjl) = (y1(Pjl), y2(Pjl), …, yn(Pjl)).
Тогда задача распознания макроструктуры заключается в отнесении каждого Plj к одному из выделенных классов {Pj} на основе его описания I(Pjl).
Решение об отнесении принимается на основе решающей функции, содержащей правила отнесения компетенции Pjl к тому или иному классу. В качестве такой функции может быть задана функция минимизации расстояния между описанием макрокомпонента и его составляющей (с использованием корреляционной метрики, меры Хемминга и т.д.).
Поскольку к рассматриваемым классам может быть отнесено достаточно большое количество составляющих, то в общем случае необходимо решить еще одну задачу: «Определение оптимальной совокупности макрокомпонентов».
При решении указанной задачи используются полученные описания макрокомпонентов I(Pj) и их составляющих I(Pjl) в пространстве выделенных признаков. На основе таких описаний с помощью метода экспертных оценок определяется весовой коэффициент значимости μl(Pj) каждой составляющей Pjl ∈ Pj для изучаемой характеристики рассматриваемого макрокомпонента Pj.
Составляющая Pjl может быть включена в 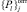 – оптимальную совокупность компетенций конкретного макрокомпонента Pj, если ее весовой коэффициент μl(Pj) будет не меньше заданного критического значения μкр.
– оптимальную совокупность компетенций конкретного макрокомпонента Pj, если ее весовой коэффициент μl(Pj) будет не меньше заданного критического значения μкр.
Таким образом, в результате решения первой подзадачи формируется представление данного объекта, оптимальное для искомой характеристики рассматриваемого объекта С на макроуровне (на уровне макрокомпонентов – {Pj}опт и их составляющих – 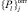 ).
).
II. Комплексная подзадача распознавания операциональной структуры объекта С
В рамках решения задачи «Формирование исходной совокупности проявлений» для обеспечения диагностики состояния или уровня развития каждого макрокомпонента {Pj}, а также всего объекта С в целом, указанный объект должен быть представлен на операциональном уровне в виде совокупности проявлений {xr}, r = 1, 2, …, k. Такими проявлениями являются поведенческие и деятельностные индикаторы, для которых выполняются следующие требования:
- однозначность понимания смысла каждого проявления;
- реальная возможность фиксации (оценки) каждого проявления [8].
Ясно, что указанная задача имеет решение, если любой макрокомпонент Pj может быть представлен соответствующими проявлениями xij, xij ∈ Pj, где i – номер проявления; j – номер макрокомпонента, к которому принадлежит проявление. Такие проявления представляют собой качественные и количественные показатели, поведенческие и/или деятельностные индикаторы, которые можно реально наблюдать и оценить.
Как было отмечено выше, в силу неопределенности и неоднозначности имеющейся информации об объекте С совокупность проявлений не может быть закрытой, имеющей наперед заданное количество элементов. Поэтому, чтобы процедура диагностики состояния или уровня развития каждого макрокомпонента описываемого объекта была выполнима, нужно отобрать минимально необходимое количество проявлений для обеспечения.
В рамках решения следующей задачи «Классификации проявлений» определяется отнесение каждого проявления к одному из выделенных классов. При этом в качестве классов выступают ранее определённые макрокомпоненты.
Каждое проявление можно описать некоторой совокупностью признаков Z = {zl}, l = 1, ..., N, представляющих те или иные характеристики (особенности) рассматриваемого макрокомпонента. Пространство этих признаков может совпадать с пространством Y признаков объекта С или расширять его за счет добавления новых признаков.
Аналогично макрокомпонентам каждое проявление xr может быть представлено своим описанием в пространстве выделенных признаков Z, характеризующим проявление xr с позиции наблюдателя:
I(xr) = (z1(xr), z2(xr), …, zN(xr)).
Тогда задача распознания операциональной структуры заключается в отнесении каждого проявления xr к выделенным классам {Pj} на основе его описания I(xr).
Традиционно при рассмотрении классической задачи распознавания [7] каждый объект-образ строго относился к одному из выделенных классов. Однако в силу нечеткости структуры слабо формализованного объекта рассматриваемые проявления не всегда можно строго отнести только к одному из макрокомпонентов. Для рассматриваемого объекта каждое проявление xr может быть отнесено к нескольким макрокомпонентам.
В силу нечеткости отнесения проявлений xr к макрокомпонентам Pj необходимо определить меру пригодности каждого проявления xr для диагностики состояния (уровня развития) рассматриваемых макрокомпонентов. Для характеристики этой меры пригодности может быть использована степень принадлежности 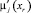 каждого проявления xr к конкретному макрокомпоненту Pj, представленная в виде значения нормированной функции принадлежности. Такая функция определяется на основе описания проявлений в пространстве выделенных признаков Z и позволяет для каждого проявления определить значения функции его принадлежности к имеющимся макрокомпонентам.
каждого проявления xr к конкретному макрокомпоненту Pj, представленная в виде значения нормированной функции принадлежности. Такая функция определяется на основе описания проявлений в пространстве выделенных признаков Z и позволяет для каждого проявления определить значения функции его принадлежности к имеющимся макрокомпонентам.
Количество проявлений, относящихся к каждому макрокомпоненту, чаще всего довольно велико. Поэтому для оценки уровня состояния и/или развития каждого макрокомпонента Pj и объекта C в целом необходимо сформировать оптимальную совокупность проявлений {xr}опт относительно всех макрокомпонентов.
В рамках задачи «Определение оптимальной совокупности проявлений» осуществляется селекция проявлений. В оптимальную совокупность {xr}опт включаются такие проявления, которые являются самыми значимыми (важными) для характеристики каждого макрокомпонента. Отбор соответствующих проявлений осуществляется на основе всех оптимальных совокупностей проявлений, сформированных для характеристики каждого макрокомпонента. При таком отборе критически важным является требование минимальности различия между величиной суммарной представленности макрокомпонентов в пространстве проявлений. В результате формируется операциональный уровень модели рассматриваемого объекта. В целом полученная модель обеспечивает возможность выполнить общую и дифференциальную диагностику состояния (уровня развития) слабо формализованного объекта С, а также его макрокомпонентов Pj и Pjl.
Результаты апробации описанной методики распознавания структуры слабо формализованных объектов применительно к структуре качества педагогической поддержки обучающихся представлены в докладе Б.Е. Фишмана и Б.С. Мердеевой «Распознавание структуры объекта с нечеткими отношениями на примере качества педагогической поддержки обучающихся» на международной научно-практической конференции «Научные исследования в сфере гуманитарных и естественных наук: междисциплинарный подход и генезис знаний» (31 мая 2016, г. Самара).
Библиографическая ссылка
Фишман Б.Е., Мердеева Б.С. МЕТОДИЧЕСКИЕ ОСНОВЫ РАСПОЗНАВАНИЯ СТРУКТУРЫ СЛАБО ФОРМАЛИЗОВАННОГО ОБЪЕКТА // Фундаментальные исследования. – 2016. – № 7-2. – С. 272-276;URL: https://fundamental-research.ru/ru/article/view?id=40497 (дата обращения: 26.04.2024).



