Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Рецензия
• Файлы
• Ключевые слова
• Литература

Кошкин Б.П. 1 Носков С.И. 1 Оленцевич В.А. 1 Рязанцев А.И. 1

---

1 ФГБОУ ВО «Иркутский государственный университет путей сообщения»

В данной статье рассматривается специальная задача линейного программирования – транспортная задача, заключающаяся в поиске наиболее экономного плана перевозки однородной, взаимозаменяемой продукции из пунктов производства в пункты потребления. Приводится математическая постановка транспортной задачи в виде замкнутой и открытой моделей, а также способ приведения открытой модели к замкнутой с введением фиктивного пункта производства или фиктивного пункта потребления продукции. Предлагается математическая постановка многокритериальной транспортной задачи с двумя целевыми функциями, заключающейся в одновременной минимизации суммарных затрат на перевозку и максимизации степени важности перевозок. Отмечается метод, который может быть использован как наиболее эффективный для решения такой задачи – многокритериальный симплекс-метод, основанный на построении множества Парето в задаче многокритериального линейного программирования.

Рецензия № 1

130 KB

Рецензия № 2

250 KB

Статья в формате PDF

0 KB

векторная оптимизация

многокритериальное линейное программирование

многокритериальный симплекс-метод

транспортная задача

транспортная модель

транспортные перевозки

целевая функция

1. Ашманов С.А. Линейное программирование [Текст] / С.А. Ашманов. – М.: Наука. Главная редакция физико-математической литературы, 1981. – 340 с.

2. Базилевский М.П., Баенхаева А.В., Носков С.И. Моделирование валового регионального продукта Иркутской области на основе применения методики множественного оценивания [Текст] // Фундаментальные исследования. – 2016. – № 10–1. – С. 9–14.

3. Гольштейн Е.Г. Задачи линейного программирования транспортного типа [Текст] / Е.Г. Гольштейн, Д.Б. Юдин. – М.: Наука. Главная редакция физико-математической литературы, 1969. – 384 с.

4. Золотарюк А.В. Математическая модель многокритериальной оптимизации транспортных перевозок [Текст] // Инновационные технологии в науке и образовании. – 2015. – № 1. – С. 317–320.

5. Константинова М.А. К вопросу многокритериальной задачи в транспортной логистике [Текст] // Научное сообщество студентов XXI столетия. Технические науки: сб. ст. по мат. XVIII междунар. студ. науч.-практ. конф. – Новосибирск: «СибАК», 2014. – № 3(18). – С. 49–54.

6. Мунасыпов Н.А. Линейное программирование [Текст]: учебное пособие / Н.А. Мунасыпов. – Оренбург: ООО «Агентство «Пресса», 2015. – 122 с.

7. Носков С.И. Точечная характеризация множества Парето в линейной многокритериальной задаче [Текст] // Современные технологии. Системный анализ. Моделирование. – 2008. – № 1. – С. 99–101.

8. Носков С.И., Баенхаева А.В. Множественное оценивание параметров линейного регрессионного уравнения [Текст] // Современные технологии. Системный анализ. Моделирование. – 2016. – № 3(51). – С. 133–140.

9. Осыкина Ю.А., Чернышова Г.Д. Многокритериальная транспортная задача с разрывной целевой функцией [Текст] // Вестник Воронежского государственного университета. Серия: системный анализ и информационные технологии. – 2008. – № 2. – С. 10–12.

10. Yu L., Zeleny M. The set of all nondominated solutions in linear cases and multycriteria simplex method // J. of Math. Anal. and Applic. – 1975. – Vol. 45, № 2. – P. 430–468.

Транспортная задача относится к типу специальных задач линейного программирования, обладающих некоторыми особенностями, с учётом которых могут быть разработаны упрощённые методы решения, значительно более экономные по сравнению с принятыми. В классической постановке транспортная задача заключается в поиске такого плана перевозок продукции одного типа (однородной, взаимозаменяемой) из пунктов производства в пункты потребления, при котором затраты на перевозку минимальны (см., например, [1, 3, 6]).

Первая строгая постановка данной задачи принадлежит Хичкоку, а её детальное рассмотрение и разбор – Купмансу. Данциг сформулировал транспортную задачу как задачу линейного программирования и разработал первые методы её решения. Многие литературные источники, посвящённые линейному программированию, так или иначе упоминают, затрагивают транспортную задачу (см., например, [1, 6]). Целиком посвящена классу транспортных задач и методам их решения монография Е.Г. Гольштейна, Д.Б. Юдина [3].

Основной целью данной статьи является описание постановки многокритериальной транспортной задачи с двумя целевыми функциями, представляющей собой усложнённую транспортную задачу линейного программирования.

Постановка транспортной задачи

Существуют замкнутая и открытая транспортная модель. Формулировка транспортной задачи в виде замкнутой транспортной модели заключается в следующем: имеется m пунктов производства 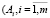) и n пунктов потребления 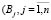) однородной, взаимозаменяемой продукции. Для каждого пункта производства заданы объёмы производства a_i, а для каждого пункта потребления – величины спроса b_j в одних и тех же единицах измерения:

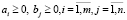
Расходы, связанные с перевозкой единицы продукта из i-ого пункта в j-ый, заданы величиной c_ij и известны для каждой пары (i, j). Можно представить эти расходы в виде матрицы размерностью m×n:

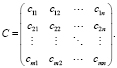
Требуется обеспечить перевозку всей продукции из пунктов производства в пункты потребления таким образом, чтобы расходы на перевозку были минимальными, т.е. план перевозки был наиболее экономным.

Искомое количество единиц продукта, поставленное из i-ого пункта в j-ый, определяется величиной x_ij. Количество перевезённой продукции неотрицательно:

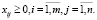
Можно представить перевезённую продукцию в виде матрицы размерностью m×n:

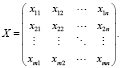
Исходные данные удобнее всего представляются в виде таблицы (таблица).

Исходные данные задачи

Математическая модель транспортной задачи имеет следующий вид.

Минимизируются суммарные расходы на перевозку всей продукции (из всех пунктов производства во все пункты потребления):

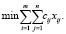
Замкнутость транспортной модели подразумевает перевозку всей продукции, имеющейся в пунктах производства и полное удовлетворение спроса на продукцию в пунктах потребления. Математически эти условия выглядят следующим образом:

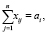
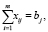
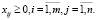
Для допустимости такой задачи необходимо и достаточно, чтобы выполнялись условия

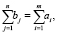
т.е. объём продукции, имеющейся в пунктах производства, должен совпадать с объёмом продукции, требуемым в пунктах потребления.

Для представления условий задачи в матричном виде требуется ввести в рассмотрение векторы Pij и Р.

Pij – вектор коммуникации, соответствующий коммуникации, которая связывает i-ый пункт производства с j-ым пунктом потребления, и состоящий из (n + m) компонент, из которых i-я и (m + j)-я равны единице, а все остальные – нулю:

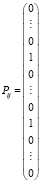
Р – вектор производства – потребления, состоящий из объёмов производства a_i и величин спроса b_j:

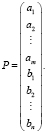
Тогда условия полного вывоза продукции из всех пунктов производства и полного удовлетворения спроса в пунктах потребления в матричной форме будут выглядеть следующим образом:

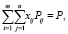
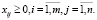
В открытой транспортной модели подразумевается, что в пунктах производства может оставаться неотправленный товар:

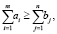
тогда справедливо следующее условие:

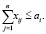
Либо имеющейся в пунктах производства продукции может быть недостаточно для полного удовлетворения спроса в пунктах потребления:

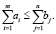
В таком случае справедливо условие

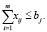
Открытую транспортную модель можно привести к замкнутой. Если объём продукции в пунктах производства больше требуемого объёма продукции на пунктах потребления, то вводится фиктивный пункт потребления B_{n +1} с объёмом потребления

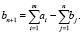
Величина b_{n +1} определяет суммарный объём нереализованного продукта.

Стоимость перевозок от каждого поставщика в такой фиктивный пункт потребления – нулевая:

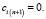
Если объём продукции в пунктах производства меньше требуемого объёма продукции на пунктах потребления, то вводится фиктивный пункт производства A_{m +1} с объёмом поставок

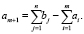
Стоимость перевозок от фиктивного поставщика в каждый из пунктов потребления нулевая:

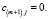
Постановка многокритериальной транспортной задачи

Существуют различные модификации транспортной задачи, в том числе и многокритериальные транспортные задачи.

В работе [9] в качестве целевой функции рассматривается минимизация максимального среди всех потребителей числа поставщиков. Несмотря на название («Многокритериальная транспортная задача с разрывной целевой функцией») решается задача при помощи стандартных методов линейного программирования.

В работе [4] в качестве условий рассмотрены: минимизация времени нахождения в пути из пункта производства в пункт потребления продукции, минимизация общей себестоимости перевозки единицы груза, максимизация общего количества перевезённых грузов. Предлагается решать задачу с использованием методов Парето, устанавливая приоритеты критериев, или с использованием интеллектуальных методов нейросетевого прогнозирования. В данном случае определение приоритетов и выделение главного критерия является одним из самых простых методов многокритериального линейного программирования.

В работе [5] минимизировать предлагается расстояние между пунктами назначения перевозки, время транспортировки груза, тарифы перевозки и стоимость перевозки. В качестве решения такой задачи рассматриваются два метода: первый, как и в работе [4], заключается в установлении приоритетов критериев и выделении главного критерия, а второй – в свёртывании критериев и введении одного агрегированного критерия.

Рассмотрим более сложную для решения модификацию транспортной задачи с двумя целевыми функциями. Для этого введём матрицу H размерностью m×n. Элемент h_ij матрицы H определяет степень важности перевозки продукта из i-ого пункта производства в j-ый пункт потребления. Степень важности перевозки для каждой пары (i, j) может задаваться, например, экспертами:

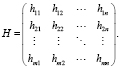
Соответственно, добавляемая целевая функция заключается в максимизации степени важности перевозок:

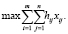
В такой постановке транспортная задача является многокритериальной, т.к. заключается в одновременной минимизации суммарных затрат на перевозку и максимизации степени важности перевозок. Математически закрытая модель многокритериальной транспортной задачи выглядит следующим образом:

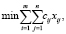
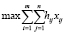
при условиях

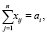
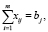
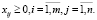
или в матричном виде:

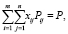
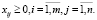
Для открытой модели многокритериальной транспортной задачи справедливо одно из условий (в зависимости от типа открытой модели):

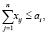
либо

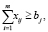
и также условие неотрицательности количества перевозимой продукции:

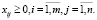
При приведении открытой транспортной модели к замкнутой важность перевозки из фиктивного пункта производства A_{m +1} или в фиктивный пункт потребления B_{n +1} будет нулевой:

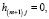
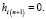
Решение поставленной задачи может быть найдено при помощи многокритериального симплекс-метода, основанного на построении множества Парето в задаче многокритериального линейного программирования [7, 8, 10].

Заключение

Рассмотрена формулировка и математическая постановка транспортной задачи линейного программирования. Предложен способ усложнения данной задачи за счёт введения дополнительной целевой функции. Отмечен метод, подходящий для решения поставленной задачи многокритериального линейного программирования.

Библиографическая ссылка