Стратегическая цель экономической политики государства в целом и налоговой политики в частности заключается в создании в России стабильной налоговой системы, которая бы обеспечила достаточный объем налоговых поступлений в бюджеты всех уровней за счет формирования эффективных механизмов налогообложения всех категорий налогоплательщиков, а также информационного обеспечения процесса принятия управленческих решений в процессе функционирования налоговой системы. Возникает необходимость обработки огромного количества информации о налогоплательщиках, имеющей количественный и качественных характер, связанной с неформализуемыми и плохо формализуемыми факторами, которую невыгодно хранить и трудно перерабатывать традиционными методами. Поэтому целесообразно воспользоваться сжатием больших объемов информации путем нахождения некоторых общих закономерностей [1]. Распределить налогоплательщиков по категориям внимания, к которым будут применяться соответствующие комплексы мероприятий с целью эффективного управления процессами в налоговой службе. Наилучший способ применить методы кластерного анализа [2, 3]. Исследованиям в данной области посвящены работы известных зарубежных и российских ученых: J.C. Bezdek, L.A. Zadeh, А.Н. Аверкина, Д.А. Вятченина, В.Д. Штовбы, А.В. Леоненкова, А.Н. Борисова, М.П. Деменкова и др.
Целью работы является проведение анализа методов кластеризации для дальнейшего применения его результатов в эффективном управлении процессами в налоговой службе.
Центральное место среди методов кластерного анализа данных занимает кластерный анализ, являющийся одним из наиболее многообещающих и наиболее интересных подходов к исследованию многомерных процессов и явлений и относящийся к одному из основных методов интеллектуальной обработки данных [4]. Его использование оправдано везде, где требуется многомерный анализ разнокачественной информации.
Задача кластеризации заключается в разбиении объектов X на несколько подмножеств, объекты в которых имеют большие сходства между собой, чем с объектами из других кластеров. «Сходство» в метрическом пространстве определяют через расстояние [5, 6].
Алгоритмы кластеризации оперируют с объектами. С каждым объектом Х отождествляется вектор характеристик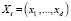 
.
Компоненты xi,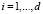 
являются отдельными характеристиками объекта. Размерность пространства характеристик определяет количество характеристик d.
Состоящее из всех векторов характеристик объектов, множество обозначается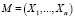 
, где 
.
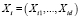Подмножество «близких друг к другу» объектов из М представляет собой кластер. Расстояние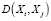 
между объектами Xi и Xj определяется в пространстве характеристик на основе выбранной метрики [7, 8].
Требования, предъявляемые к выявлению кластеров в исследуемой совокупности объектов:
– представление каждого кластера должно быть выражено однородной категорией, содержащей похожие объекты по близким значениям свойств или признаков;
– исследуемая совокупность всех объектов должна быть распределена по всем кластерам, иными словами, быть исчерпывающей;
– каждый объект исследуемой совокупности не должен принадлежать одновременно двум разным кластерам, т.е. кластеры должны быть взаимно исключающими.
Исходной причиной разработки большого многообразия алгоритмов и методов кластеризации послужила возможность использования различных подходов к формальному определению кластеров. Алгоритмы и методы кластерного анализа как инструмент предварительного анализа данных незаменимы при поиске закономерностей в больших наборах многомерных данных, таких как хранилища данных [9]. Именно поэтому для распределения налогоплательщиков по категориям внимания в данной работе предложен метод кластерного анализа. Несмотря на то, что на сегодняшний день известны сотни алгоритмов и методов кластеризации, не существует «универсального решения», поскольку специфика поставленной задачи характеризуется спецификой объекта кластеризации.
Исходя из того, что объектом кластеризации являются данные о налогоплательщиках, требования, которым должен удовлетворять используемый метод кластеризации, сформулированы следующим образом:
– Высокая размерность пространства данных – объекты описываются большим количеством атрибутов, следовательно, должна быть приспособленность алгоритма к работе в пространствах данных высокой размерности.
– Большой объем данных – в связи с тем, что информация о налогоплательщиках обновляется каждый отчетный период, увеличивая тем самым исходную выборку, необходимо, чтобы алгоритм был масштабируем для работы с большим объемом данных.
– Смешанный тип измерений – описание поведения налогоплательщиков включает в себя количественные и качественные характеристики, поэтому алгоритм должен быть приспособлен к использованию различных типов измерений.
По способу обработки данных методы кластерного анализа подразделяются на иерархические и неиерархические. В иерархических методах выполняется последовательное объединение меньших кластеров в большие или же наоборот, большие разделяются на меньшие. Из таких методов выделяют агломеративные, характеризующиеся последовательным объединением исходных элементов и уменьшением числа кластеров, выполняемым до тех пор, пока все элементы не будут принадлежать одному кластеру, и дивизимные, характеризующиеся последовательным разбиением исходного кластера, состоящего из всех объектов, с соответствующим увеличением числа кластеров. Наиболее широко известные из агломеративных методов CURE, ROCK, CHAMELEON и др., а среди дивизимных – BIRCH, MTS и др. Вышеперечисленные методы обладают рядом достоинств и недостатков. Так, например, CURE формирует кластеры несферической формы различных размеров и плотности, однако требует задания некоторых порогов плотности объектов и количества кластеров, а это не всегда приемлемо. ROCK применяет для кластеризации пространств со смешанными типами измерений понятие степени связи между объектами – количество их общих соседей, качество кластеризации определяется оценочной функцией, не масштабируем для большого количества объектов. CHAMELEON – производный метод кластеризации, основанный на устранении методов CURE и ROCK, использует динамическое моделирование для слияния двух кластеров, что облегчает исследование натуральных и гомогенных кластеров, однако сложен и зависим от времени.
BIRCH относится к дивизимным методам кластеризации и позволяет обрабатывать большие объемы данных, используя ограниченный объем памяти, в работе основывается на факте неоднородного распределения данных, а также обрабатывает области с большой плотностью как единый кластер, однако позволяет обрабатывать только числовые значения, выделяя кластеры выпуклой или сферической формы, а также существует необходимость задания пороговых значений. MTS позволяет выделять кластеры произвольной формы, в том числе кластеры выпуклой и вогнутой форм, выбирает из нескольких оптимальных решений самое оптимальное, но чувствителен к выбросам [10].
В неиерархических или итеративных методах кластеры формируются в зависимости от задаваемых условий разбиения с возможностью изменения пользователем с целью достижения желаемого результата. К таким методам относятся: k-средних (k-means), CLOPE, PAM, самоорганизующиеся карты Кохонена др. Метод k-средних – достаточно прост и быстр в использовании, алгоритм прозрачен и понятен, но слишком чувствителен к выбросам, на больших базах данных медленен в работе. Недостатком его является невозможность применения на пересекающихся кластерах и необходимость задания количества кластеров. У CLOPE можно отметить высокую масштабируемость и скорость работы, удобство подбирать автоматически количество кластеров, но но слишком чувствителен к выбросам. PAM – так же, как и k-means, прост и быстр в использовании, алгоритм менее чувствителен к выбросам, однако присутствует необходимость задания количества кластеров и медленная работа на больших базах данных. Самоорганизующиеся карты Кохонена используют универсальный аппроксиматор – нейронную сеть, метод прост в реализации, но позволяет работать только с числовыми данными, существует необходимость минимизации размеров сети.
По количеству применений алгоритмов кластеризации выделяют методы с одноэтапной и с многоэтапной кластеризацией.
По возможности расширения объема обрабатываемых данных различают методы масштабируемые и немасштабируемые.
По времени выполнения кластеризации методы можно разделить на потоковые (on-line) и непотоковые (off-line) [11].
По способу анализа данных методы кластеризации подразделяют на четкие и нечеткие. Четкие методы кластеризации разбивают первоначальное множество объектов X на несколько непересекающихся подмножеств. При этом любой объект с X принадлежит только одному кластеру. В результате использования нечетких методов кластеризации возможна одновременная принадлежность нескольким или даже всем кластерам, но с разной степенью принадлежности. Во многих ситуациях нечеткая кластеризация более «естественная», чем четкая, например, для объектов, расположенных на границе кластеров [6]. Нечеткая кластеризация получила широкое применение и развитие благодаря Бездеку и его метода нечетких с-средних (Fuzzy c-means – FCM), который позволяет выделять в кластер объекты, находящиеся на границе кластера, для него характерна меньшая чувствительность к выбросам, однако присутствует необходимость задания количества кластеров, вычислительная сложность кластеризации, а также возникает неопределенность с объектами, удаленными от всех центров кластеров [12].
Требование нахождения однозначной кластеризации элементов исследуемой проблемной области является достаточно грубым и твердым, особенно при решении плохо или слабо структурированных задач. Методы нечеткой кластеризации ослабляют это требование. При введении в рассмотрение нечетких кластеров и соответствующих им функций принадлежности, принимающих значения из интервала [0,1], происходит ослабление этого требования. А элементы матрицы степеней принадлежности четкого разбиения принимают значения из двухэлементного множества {0,1}, а не из интервала [0,1].
Алгоритм FСМ для решения задачи нечеткой кластеризации имеет итеративный характер последовательного улучшения некоторой исходной нечеткой разметки, которая задается пользователем или формируется автоматически по некоторому эвристическому правилу. Значения функций принадлежности нечетких кластеров и их типичные представители пересчитываются на каждой итерации. Определяется в форме итеративного выполнения последовательности шагов. Алгоритм FСМ закончит работу в случае, когда состоится выполнение заданного априори некоторого конечного числа итераций или когда минимальная абсолютная разница между значениями функций принадлежности на двух последовательных итерациях не станет меньше некоторого априори заданного значения [9].
В базовом алгоритме нечетких с-средних расстояние между объектом и центром кластера рассчитывается через стандартную Эвклидову норму. В результате выполнения алгоритмов кластеризации с фиксированной нормой форма всех кластеров получается одинаковой. Алгоритмы кластеризации как бы навязывают данным несвойственную им структуру, что иногда приводит к неоптимальным результатам [6]. Для устранения этого недостатка существует несколько методов, среди которых выделим алгоритм Густафсона – Кесселя.
Относительно алгоритма с-средних главное изменение заключается во введении в формулу расчета расстояния между векторами масштабируемой матрицы B. Алгоритм Густафсона – Кесселя использует адаптивную норму для каждого кластера, то есть для каждого i-го кластера существует своя норм-порождающая матрица. В этом алгоритме при кластеризации оптимизируются не только координаты центров кластеров и матрица нечеткой разбивки, но также и норм-порождающие матрицы для всех кластеров. Это позволяет выделять кластеры различной геометрической формы [6].
Состоит алгоритм Густафсона – Кесселя из следующих шагов.
Шаг 1. Генерирование матрицы нечеткого разбиения.
Шаг 2. Расчет центров кластеров:
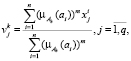(1)
где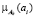 
– степень принадлежности ai-го элемента k-му кластеру;
n – общее количество объектов данных;
q – общее количество измеримых признаков объектов;
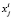– количественное значение признака 
;
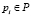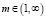– экспоненциальный вес, определяющий нечеткость, размытость кластером и равный действительному числу (m > 1).
Шаг 3. Определение матрицы ковариации для k-го кластера:
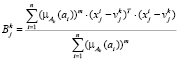. (2)
Шаг 4. Расчет расстояния между объектами из Х и центрами кластеров:
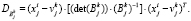(3)
Шаг 5. Перерасчет элементов матрицы нечеткого разбиения.
Если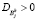 
, то проводим расчет по формуле
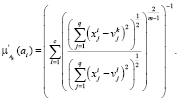(4)
Если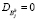 
, то для соответствующего нечеткого кластера 
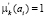, а для других 
.
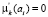Шаг 6. Проверка условия
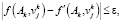
где
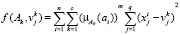. (5)
Если условие выполняется, то «конец», а иначе – к шагу 2.
Для оценки качества кластеризации можно использовать величину силуэта S. При нечеткой кластеризации номер кластера определяется по максимальному значению степени принадлежности. Значение силуэта выражается для каждого объекта следующим образом:
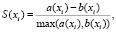(6)
где a(xi) – среднее расстояние между объектом xi (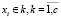
) и объектами того же кластера k, к которому принадлежит xi;
b(xi) – минимальное расстояние между объектом xi и объектами в кластере, который ближе всего к кластеру k, то есть кластер, к которому xi не принадлежит.
Значение силуэта лежит в интервале [–1; 1], если оно отрицательное, то налогоплательщик считается плохо кластеризованным.
Выводы
Таким образом, проведен анализ методов кластеризации и осуществлен выбор подходящего в соответствии с поставленными требованиями для распределения налогоплательщиков по категориям внимания. Следует отметить, что это лишь один из этапов обработки данных о налогоплательщиках. Для принятия эффективных управленческих решений в налоговой службе необходимо выполнение полного комплекса мероприятий обработки данных и создание информационной управленческой системы, что является перспективным направлением для дальнейшего исследования.
Библиографическая ссылка
Заболотникова В.С., Ромашкова О.Н. АНАЛИЗ МЕТОДОВ КЛАСТЕРИЗАЦИИ ДЛЯ ЭФФЕКТИВНОГО УПРАВЛЕНИЯ ПРОЦЕССАМИ В НАЛОГОВОЙ СЛУЖБЕ // Фундаментальные исследования. – 2017. – № 9-2. – С. 303-307;URL: https://fundamental-research.ru/ru/article/view?id=41744 (дата обращения: 16.04.2024).