Шифрование компьютерной информации является одним из инструментов борьбы с угрозами информационной безопасности, актуальность которой рассмотрена в [1, с. 109; 2] и тысячах других публикаций в научной литературе: в научных журналах, патентах и др., многие из которых являются опубликованными в последние годы.
В данной работе рассматриваются подходы к усовершенствованию криптографической системы [3, с. 139; 4], построенной на принципах, о некоторых из которых впервые сообщается в [5, с. 44]. Данная система применяет симметричный блочный алгоритм шифрования [6, с. 2] с использованием пароля, основанный на аналитических преобразованиях. В исходной системе выявлена уязвимость, связанная с проблемой известного открытого текста [7, с. 821], а также не обеспечивается восстановление большей части информации при повреждении зашифрованных данных.
Цель работы – модернизация криптографической системы для устранения вышеуказанных замечаний. Задачи: разработать модели шифрования на сетях Петри и провести анализ с помощью вычислительного эксперимента.
Модель системы в первоначальном виде
Модель шифрования предлагается построить на математическом аппарате сетей Петри, с помощью которого моделируются события в дискретных системах. Этот математический аппарат позволяет наглядно представить динамику событий в системе, проводить анализ системы и иногда применяется для моделирования шифрования [8, с. 70; 9, с. 1372; 10, с. 317]. Исходный текст обозначим {B}, зашифрованный – {S}. Модель шифрования, применяемая в исходной системе, на основе представления сети Петри в виде полинома [11, с. 57], называемого также алгебраическим представлением [12, с. 299], имеет следующий вид:
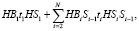
где N – число блоков, которые составляют {B};
Bi – позиция, в которой содержится метка, представляющая i-й блок {B},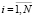 
;
Si – позиция, предназначенная для получения метки, соответствующей i-му блоку {S},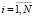 
;
H – позиция, содержащая метку, моделирующую хэш-функцию от пароля h;
ti – переход, означающий преобразование информации (операцию по шифрованию содержимого) для i-го блока,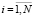 
.
Начальная маркировка –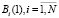 
. По окончанию срабатывания всех переходов {S} будет содержаться последовательно в совокупности позиций Si, 
.
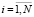Модель отчасти условна, практически используются дополнительные преобразования, о которых сообщается в некоторых публикациях по данной конкретной криптосистеме, так как иначе, зная B1 и S1, нетрудно определить значение h и в дальнейшем использовать его для подмены сообщений.
Проблемы при использовании исходной системы
В рассмотренной криптографической системе выявлена уязвимость. Для её иллюстрации рассмотрим, какими могут быть {B}. Часто различные {B} начинаются с одних и тех же групп символов, которые обозначим A. Например, сообщением может быть текст письма, начинающийся со слов приветствия, заголовок какого-либо файла и т.п. Тогда, если длина A не менее размера блока, т.е. l(A) ≥ l(B1), то S1 в различных {S} будут одинаковы.
Предположим, при передаче сообщений у злоумышленника имеется возможность чтения S1 и каким-либо образом он получил B1 одного из двух сообщений. Это соответствует проблеме известного открытого текста. Тогда, при условии, что S1 в этих двух сообщениях совпадают, злоумышленнику становится известным B1 второго сообщения. Кроме того, даже если у злоумышленника не было B1, он может сравнивать между собой только S1 разных сообщений и делать вывод об идентичности B1.
Вторая проблема относится к вопросу о целостности хранимых данных. Возможны случаи повреждения зашифрованных данных. Это характерно для таких ситуаций, как появление сбойных секторов на жестком диске, где хранится зашифрованный файл. У флеш-памяти, как альтернативы, ограничено количество циклов стирания-записи и срок хранения. Файл можно восстановить специальными системными программами, но на месте сбоя он будет искажен. Однако обычный текст содержит много избыточных данных, поэтому иногда можно воспользоваться даже частью полного сообщения для принятия верного решения в той или иной ситуации. Нужная информация может оказаться в неповрежденных участках. Другой пример – передача зашифрованной информации с помощью радиоволн в условиях боевых действий при намеренном частичном искажении передаваемых сигналов противником. На тему борьбы со сбоями при шифровании известны такие исследования, как [13].
Исследуем случай повреждения одного блока, хранящего Sk, k → [1, N]: Sk→Sk’. В исходной криптографической системе, так как содержимое блоков {S} зависит от содержимого предыдущих блоков, расшифровка {S} возможна только до Sk’. Пусть события повреждений различных блоков равновероятны:
p(Sk→Sk’) = 1/N ∀k∈[1, N].
Тогда, зная пароль, среднестатистически можно расшифровать около половины данных {S}, расположенных последовательно от его начала. Точнее, в среднем доля расшифровываемых данных по отношению к длине сообщения, обозначаемая R, составляет
R = (N–1)/2N.
Такая же проблема характерна и для некоторых других систем, используемых для шифрования. Для примера небольшой текст заархивирован в программе 7-Zip с паролем без сжатия. Затем с помощью программы Far Manager изменены ближе к концу полученного файла всего два бита: вместо символа «1» помещен «2». При извлечении из архива получено сообщение «Ошибка CRC для зашифрованного файла», файл распакован, причем ближе к концу содержимое абсолютно искажено. А при изменении символа, находящегося ближе к началу архива, кроме области заголовка, полностью искажается практически все содержимое. Следовательно, при одиночном равновероятном по всей длине повреждении {S} в этой программе в среднем становится невозможным расшифровать около ½ файла.
Устранение выявленных проблем
Пусть перед шифрованием {B} известно целиком. Для увеличения R данные в {B} представим в виде дерева иерархии блоков, распределение по которому должно быть сделано перед шифрованием на основе h, чтобы искажения в блоках не влияли на это распределение. На рис. 1 приведен пример иерархической модели шифрования на основе сети Петри.
Срабатывание любого перехода (кроме T0) в модели, изображенной на рис. 1, соответствует генерации Si из Bi, h и информации, полученной из предыдущего блока (за исключением первых четырех блоков, так как для них предыдущих блоков нет), а также генерации информации для следующих блоков. Срабатывание перехода T0 моделирует запуск процесса шифрования. После срабатывания всех переходов {S} будет содержаться последовательно в совокупности позиций S1, …, S12.
Рассчитаем R при порождении каждым блоком, не являющимся листом дерева, двух блоков и двух уровнях иерархии (рис. 1). Всего N = 12: четыре блока первого уровня и восемь – второго. Вероятность p(Si→Si’) = 1/12∀i∈[1, 12]. При повреждении блока первого уровня теряются данные его самого и последующих двух блоков поддерева, т.е. 3 из 12. Это значит, что отношение размера поврежденной части к длине всех данных l1 = 3/12. Такое возможно четыре раза из 12. Когда повреждается блок второго уровня, искажаются только его данные, т.е. l2 = 1/12. Такое возможно восемь раз из 12. По формуле полной вероятности
R = (12 – (4l1+8l2))/12 =1 – 20/144 ≈ 0,86.
Это значение существенно выше того, что наблюдается в исходной криптографической системе, что оправдывает использование данного подхода. Число уровней иерархии не ограничивается двумя, что приводит к еще более высоким показателям.
Экспериментальная часть
В среде Turbo Delphi разработан прототип компьютерной программы, реализующий модель рис. 1 при N = 2722. Каждый блок связан не более чем с одним предком и не более чем с двумя блоками-потомками, которые шифруются с использованием алгоритмов получения хэш-функции [3, с. 139] и скремблирования [4] исходной криптографической системы. Из файла с {B} последовательно отбираются фрагменты размером 2722 блока. При этом очередной фрагмент разбивается на четыре бинарных поддерева, содержащих блоки, затем шифруется и дописывается в конец выходного файла. Если размер последнего фрагмента файла меньше, чем 2722 блока, но больше четырех блоков, то он тоже разбивается на четыре поддерева. Поддеревьев четыре для того, чтобы сбой блока в корне дерева не приводил к тотальной потере информации при небольших файлах.
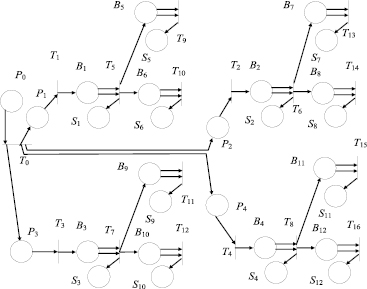
Рис. 1. Иерархическая модель шифрования: Bi – позиции с меткой, представляющей i-й блок {B}, i = 1, … 12; Si – позиции для получения метки, соответствующей i-му блоку {S}, i = 1, … 12; Ti – переходы, i = 0, … 16; Pi – позиции, моделирующие готовность и начала поддеревьев, i = 0, … 4
Рис. 2. Исходное изображение
Рис. 3. Изображение после искажения 10 байтов
Программный прототип протестирован на архивных файлах. После расшифровки архиваторы сообщений об ошибках в файле не выдают, а это значит, что ни один бит не искажается, т.е. информация расшифровывается корректно. Выполнено искусственное искажение зашифрованного данной программой файла, чтобы визуально проконтролировать изменения в получаемом после расшифровки файле. С этой целью использовано изображение (рис. 2) формата BMP (несжатое) с глубиной цвета 24 бита на пиксель, имеющее размер с заголовком 85594 байт (438×65 пикселей).
На рис. 3 изображен рисунок, полученный из исходного следующим образом:
1) шифрование прототипом программы;
2) псевдослучайное искажение 10 байтов в случайных позициях в зашифрованном файле (кроме первых 50 байт, соответствующих стандартному заголовку BMP-файла);
3) расшифровка.
Из рис. 3 видно, что большинство данных остались доступными для визуального восприятия, тогда как, например, применение для шифрования архиватора 7-Zip с паролем приводит к тому, что в среднем при аналогичных искажениях остаются доступными только 10 % данных.
Используемая модель позволяет также бороться с проблемой известного открытого текста. Совпадение исходного содержимого первого по расположению блока {S} с содержимым первого блока, полученного каким-либо образом злоумышленником, редко приводит к выявлению этого факта, так как первый блок редко является корнем дерева и шифруется с применением значения хэш-функции, получаемого на основе отличающихся в разных сообщениях блоков выше по иерархии.
Если раньше злоумышленник проводил криптографический анализ с начала файла, то теперь это значительно труднее, так как номера первых блоков иерархии вычисляются на основе h от пароля. Может быть сделана попытка поблочного сравнения содержимого блоков {S} с тем, что имеет злоумышленник, однако вероятность идентичности содержимого блоков двух разных {B} в произвольном месте файла значительно ниже, чем в самом начале, если {B} не относится к массовым рассылкам.
Усовершенствование ранее разработанного метода
При визуальном контроле результатов работы исходной криптографической системы установлено, что искажения файла слабо влияли на результат расшифровки. Количество искаженных байтов достигало нескольких сотен на 83-кбайтном изображении, и все они выглядели как отдельные точки. Поэтому алгоритм [4] изменения подстановочной последовательности при реализации иерархической модели шифрования изменен следующим образом.
Во-первых, в каждых восьми последовательных байтах сообщения при шифровании производится транспонирование соответствующей битовой матрицы размером 8×8.
Во-вторых, если ранее у виртуального прямоугольного параллелепипеда размером 4×6×15, на котором размещались 256 кодов символов, для преобразования подстановочной последовательности циклически сдвигались только отдельные его слои, то теперь сдвигается весь остаток параллелепипеда от текущего отсчета координаты до окончания фигуры.
В-третьих, содержимое грани указанного окончания движется по часовой стрелке так, что при каждом единичном сдвиге слоев коды символов на краях грани тоже сдвигаются на единицу. Коды символов, которые на единицу ближе к центру грани, сдвигаются один раз за два единичных сдвига слоев. На грани размером 6×15 имеются коды символов, которые на две единицы ближе к центру. Они сдвигаются один раз за три единичных сдвига слоев.
В результате указанных исправлений шифрование стало более эффективным, что выражается в появлении значительного количества искажений после расшифровки при внесении даже небольших искажений в зашифрованный файл, как это видно из рис. 3.
Заключение
Таким образом, для модернизации разработанной ранее криптографической системы имеет смысл использовать предлагаемую иерархическую модель шифрования. Она позволяет в большинстве случаев решить проблему известного открытого текста, а также практически всегда восстанавливать большую часть исходной информации после небольших повреждений зашифрованных файлов. Произведенные усовершенствования ранее разработанного метода изменения подстановочной последовательности позволяют добиться более эффективного шифрования.
Библиографическая ссылка
Димитриев А.П. МОДИФИКАЦИЯ МЕТОДА ШИФРОВАНИЯ ДЛЯ СОКРАЩЕНИЯ ПОТЕРЬ ДАННЫХ ПРИ ИХ ПОВРЕЖДЕНИИ // Фундаментальные исследования. – 2017. – № 11-1. – С. 58-62;URL: https://fundamental-research.ru/ru/article/view?id=41898 (дата обращения: 03.12.2024).