Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Файлы

Рыкова Е.В.

Статья в формате PDF

284 KB

Семантическая информация в работе [1] определяется как «Выраженные знаками сведения о выделенной заданием стороне (сторонах) объекта».

Предметом исследования в информационных семантических системах является цель, содержание и форма представления информации. Н.М. Соломатин рассматривает четыре основных формы представления семантической информации:

t - текстовая форма (t-форма) представления;

S - аудиальная (речь, звуки) форма (S-форма);

g - визуальная (жесты, пластика) форма (g-форма);

С - изобразительная, графическая форма (С-форма).

Очевидно, что в каждом конкретном случае используется ограниченный набор средств представления семантической информации в каждой из однородных форм представления. Множество средств представления в каждом конкретном случае можно рассматривать как базовый набор в рассматриваемой ситуации - базисные векторы e_i.

Определим вектор e₁= e_t как актуальное подмножество множества текстовых форм представления, т. е. множество, используемое в исследуемой ситуации. Аналогично определим e₂= e_S, e₃= e_g, e₄= e_C. Такая форма записи позволяет рассматривать информацию как результат разложения информации P по векторам базиса в каждом конкретном случае ее представления

P = Pⁱ e_i = P^ij e_i e_j = P^ijk e_i e_j e_k = L

Для краткости мы здесь используем правило суммирования по повторяющимся дважды индексам. Совокупности величин Pⁱ, P^ij, P^ijk - конкретные представления информации при использовании унарной, бинарной и тернарной форм.

Одним из фундаментальных принципов теории информационных семантических систем является принцип инвариантности: семантическая информация об объекте остается неизменной независимо от форм ее представления [1]. Как известно, тензорные величины и связанный с ними закон преобразования являются следствием требования инвариантности некоторых объектов (векторов) относительно допустимых координатных преобразований. Это обстоятельство позволяет обратиться к тензорной алгебре как к форме описания информационных семантических систем.

Приращение информации может происходить как вследствие расширения содержания информации, т.е. слияния нескольких информационных потоков, так и вследствие изменения базиса. Пусть P - некоторая информация, содержание которой не изменяется, и, следовательно, приращение ее при переходе от одной точки информационного пространства к другой (бесконечно близкой) должно быть равно нулю. Тогда

(1)

Здесь знаком «~» (тильда) обозначена производная от проекции информации на векторы базиса при неизменном ее содержании. Последнее слагаемое обусловлено изменением базиса при переходе в соседнюю точку информационного пространства. Само изменение базиса также представляет собой семантическую операцию и, вследствие этого, производные от векторов базиса могут быть спроектированы на сами векторы базиса

(2)

где  элементы представления изменений базиса средствами исходного базиса. С учетом (2) выражение (1) преобразуется к виду

,

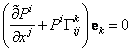откуда следует, что

и приращение представления информации в базисе вследствие его изменения  равно

(3)

В дифференциальной геометрии величины  называют коэффициентами аффинной связности. Таким образом, соотношение (3) позволяет определить информационное семантическое пространство как пространство аффинной связности [2].

СПИСОК ЛИТЕРАТУРЫ

1. Соломатин Н.М. Информационные семантические системы. - М.: Высшая школа, 1989. - 127 с.
2. Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1964. - 664 с.

Библиографическая ссылка