В процессе проектирования техническую систему S можно представить в виде совокупности некоторых элементов множества G и взаимосвязей между этими элементами из множества Q, т.е.:
Gi - i-ое подмножество взаимозаменяемых элементов множества G (i = 1, ..., n; gi ∈Gi), Qij -подмножество взаимозаменяемых связей i-го элемента с другими j = 1, ..., n (i ≠ j) элементами множества G (qij ∈ Qij).
S =<g 1, ..., gn; q 12, ..., q1 n; ...; q1 k, .., qnk; ...; q1 n, .., qnn-1>, (1)
где G = {G1,..., Gn},
Q = {Q12, ..., Q1n; ...; Q1k , ..., Qkn ; ...; Q1n, ..., Qnn-1},
Отсутствие связей q11, ..., qkk; ...; qnn говорит о невозможности влияния на функционирование любого элемента множества G этого же элемента. Взаимозаменяемость означает, что из подмножества Gi можно применить любой из элементов, а из подмножества Qij любую реализуемую на практике связь при создании системы (1). При этом любой из элементов множества G, как и любая связь из множества Q, может отсутствовать в проектируемой системе S.
Для определенности считаем, что все связи стационарные. Влияние связей на функционирование системы S, как правило, описывается конструктивными параметрами и характеристиками, включаемыми в множество параметров и характеристик элементов множества G. Следовательно, каждому элементу множества gi соответствует множество конструктивных параметров Ki и характеристик Xi, а связи из множества Q будут определять только структуру технической системы S: gi=gi(Ki , Xi ).
Математические модели Mi функционирования технической системы S в различных условиях эксплуатации, сложность, инвариантность, полнота и адекватность моделей во многом определяются множествами G и Q, т.е.:
Mi = Mi(G1,., Gn; Q12, ...,Q1n; ...;Q1k , ...,Qnk; ...;Q1n , ...,Qnn-1). (2)
В общем случае процесс структурно-параметрической оптимизации многокритериальный и базируется на векторном критерии эксплуатационных показателей и характеристик ![]() технической системы S, в основу расчета которого положены математические модели (2). Следовательно,
технической системы S, в основу расчета которого положены математические модели (2). Следовательно,
![]()
В соответствии с изложенным, определение оптимального технического решения Sîïò для заданной совокупности элементов множества G и взаимосвязей между этими элементами из множества Q для технической системы (1) сводится к определению оптимума векторного критерия ![]() по множествам конструктивных параметров Ki и характеристик Xi [1, 2]:
по множествам конструктивных параметров Ki и характеристик Xi [1, 2]:
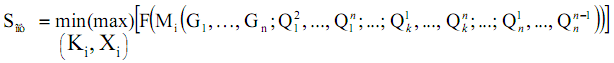
Для решения задачи структурно-параметрической оптимизации в целом предлагается принцип дискретного изменения составляющих элементов g1, ..., gn технической системы S из множества G и связей q12, ..., q1n; ...; q1k, ..., qnk; ...; qn1, ..., qnn-1 из множества Q, т.е. принцип перебора различных структурных схем и определение оптимального параметрического решения для каждого возможного исполнения технической системы (1). Дальнейший анализ оптимальных решений для всех возможных конструктивных исполнений технической системы S позволяет окончательно принять научно-обоснованное техническое решение.
Синтез конструкции и структурно-параметрическая оптимизация сложных технических систем при создании изделий, соответствующих мировому техническому уровню, возможны только на основе современных компьютерных систем и технологий, базирующихся на методах математического моделирования и многокритериальной оптимизации. В настоящее время изложенный формализованный процесс структурно-параметрической оптимизации применяется при выполнении проекта "Разработка научных основ расчета, проектирования и конструирования гибридных энергосиловых установок (ГЭСУ) транспортных машин и создание экспериментального образца городского автомобиля особо малого класса (квадрицикла) с ГЭСУ", выполняемого в соответствии с разделом "Проведение фундаментальных исследований в области естественных, технических и гуманитарных наук" программы Министерства образования и науки Российской Федерации "Развитие научного потенциала высшей школы (2006-2008 годы)".
СПИСОК ЛИТЕРАТУРЫ
- Кондрашкин А.С., Умняшкин В.А., Филькин Н.М. Оптимизация параметров транспортных средств в условиях многокритериальности// Проблемы совершенствования автомобильной техники: Тезисы докладов Всесоюзного семинара. - М.: МВТУ, 1986. - С. 56-57.
- Филькин Н.М. Методики оптимизации параметров конструкции энергосиловой установки транспортной машины. - Ижевск: ИжГТУ, 2001. - 79 с.
Работа представлена на заочную электронную конференцию с общероссийским участием «Фундаментальные исследования», 15-20 февраля 2006г. Поступила в редакцию 14.08.06г.
Библиографическая ссылка
Филькин Н.М., Хамидуллин Р.П. ФОРМАЛИЗАЦИЯ ПРОЦЕССА СТРУКТУРНО-ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИИ ТЕХНИЧЕСКИХ СИСТЕМ // Фундаментальные исследования. – 2006. – № 11. – С. 79-80;URL: https://fundamental-research.ru/ru/article/view?id=6553 (дата обращения: 26.04.2024).



