Среди показателей качества встречаются величины, не имеющие количественной меры (например, появление брака, наличие дефектов). Чтобы количественно выразить зависимость этих показателей от технологических величин, необходимо определить вероятность их появления при различных режимах обработки Pc. Математическую модель, дающую оценку Pc по значениям технологических величин, запишем в виде [1]
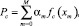
гдe fc(xm) – оптимальные функции связи между откликом и технологическими величинами, m – количество технологических величин, m = 0, 1, ..., M; αm – коэффициенты модели, вычисляются любым способом, например при помощи МНК.
Построение моделей начинается с построения сетки – разбиения пространства параметров Ξ на множество подпространств (альтернатив) Ξμ, образованных сочетаниями алфавитов технологических величин x[t] [2–6]:
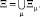
Сетка – набор подпространств. Наиболее равномерный просмотр n-мерного куба обеспечивает кубическая решетка. Поэтому при построении моделей строятся сетки в множествах простой структуры (куб, параллелепипед).
На первом этапе для каждой случайной технологической величины определяются минимальные и максимальные значения по исследуемой выборке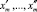 
. Затем этот диапазон изменения входной величины разбивается на ряд составляющих алфавитов: 
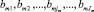, где, m – случайная величина, jm = 1, ..., Jm – номера составляющих алфавита данной величины. Каждая выделенная составляющая алфавита
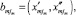
где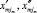 
– границы выделенной jm-й составляющей алфавита. Середины алфавитов – 
.
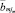Пример построения сетки для двумерного случая приведен на рис. 1.
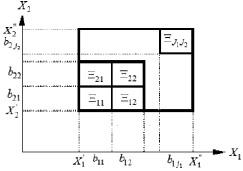
Рис. 1. Двумерная сетка множества подпространств (альтернатив) Ξμ
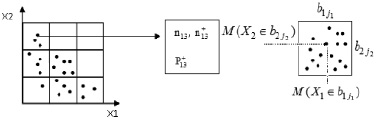
Рис. 2. Пример распределения случайных величин по подмножествам Ξμ: n1,3 – количество попаданий в подмножество Ξ1,3;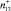 
– количество попаданий, характеризующихся возникновением дефектов; 
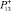– частота возникновения дефекта
При реализации технологии значения случайных величин xi будут распределяться по подмножествам Ξμ (рис. 2).
Частота возникновения дефекта для каждого подмножества Ξμ:
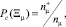
где nμ – количество попаданий в подмножество Ξμ; 
– количество попаданий, характеризующихся возникновением дефектов.
Для построения моделей формируется выборка на основе полученных результатов. Можно использовать несколько способов ее формирования.
1 способ
Каждое подмножество Ξμ рассматривается как одна точка выборки вне зависимости от того, сколько точек в нём находится. В качестве входов модели выступают значения середин алфавитов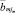 
, формирующих соответствующее подмножество. В качестве выхода – частота возникновения дефекта данного подмножества Pc(Ξμ).
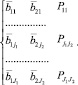
Во всех рассматриваемых случаях, если количество попаданий в подмножество равно нулю или ниже задаваемого порогового значения, данное подпространство не рассматривается и его результаты не включаются в формируемую выборку.
2 способ
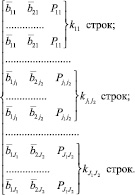
Так как количество попаданий в подпространства различно, то количество строк формируемой выборки от каждого подпространства должно быть кратным пороговому значению. То есть если в подпространство попало, например, 5 точек и порог равен 5, то включается в выборку одна точка, а если попало 15 точек, то включается 3 строки с одинаковыми значениями входов (координат подпространства) и выхода (частоты возникновения дефекта данного подмножества).
Одно подпространство рассматривается как несколько точек.
Число точек определяется по формуле
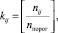
здесь квадратные скобки означают целую часть дроби.
3 способ
Отличие способа 3 от способа 2 заключается в том, что в качестве входов вместо координат подпространств выступают средние значения случайных величин в рассматриваемом подпространстве.
4 способ
В отличие от 2 и 3 способов количество строк формируемой выборки от каждого подпространства должно быть равно количеству попаданий в подмножество (nμ). Координатами входов для всех этих точек будут являться координаты подпространства (как в способе 2) или средние значения случайных величин в рассматриваемом подпространстве (как в способе 3).
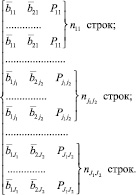
5 способ
Как и в способе 4, количество строк формируемой выборки от каждого подпространства должно быть равно количеству попаданий в подмножество (nμ), но координатами входов будут реальные значения точек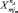 
, попавших в подпространство, а выходами (как и во всех предыдущих случаях) частоты возникновения дефекта данного подмножества.
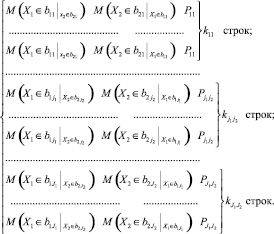
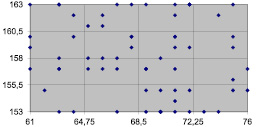
Рис. 3. Распределение точек по интервалам
Координаты подпространств и количество попаданий
|
Ξμ |
1,1 |
1,2 |
1,3 |
1,4 |
2,1 |
2,2 |
2,3 |
2,4 |
3,1 |
3,2 |
3,3 |
3,4 |
4,1 |
4,2 |
4,3 |
4,4 |
|
nμ |
3 |
1 |
9 |
4 |
3 |
6 |
3 |
2 |
3 |
2 |
3 |
2 |
3 |
5 |
4 |
2 |
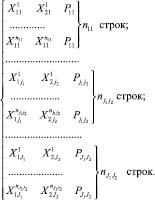
Пример распределения точек приведен на рис. 3. Координаты подпространств и количество попаданий представлены в таблице.
Если принять пороговое значение равным 3, то подпространства с координатами (1,2), (2,4), (3,2), (3,4), (4,4) участвовать в формировании выборки не будут.
(0–2 точки = 0; 3–5 точек = 1 запись; 6–8 точек = 2 записи; 9–11 точек = 3 записи).
Заключение
Предложена методика построения моделей зависимости показателей, не имеющих количественной меры, от технологических величин. Рассмотрены способы формирования исходной выборки для построения моделей.
Библиографическая ссылка
Корнеев А.М., Аль-Сабри Г.М., Омельянчук В.В. МОДЕЛИ ЗАВИСИМОСТИ ПОКАЗАТЕЛЕЙ, НЕ ИМЕЮЩИХ КОЛИЧЕСТВЕННОЙ МЕРЫ, ОТ ТЕХНОЛОГИЧЕСКИХ ВЕЛИЧИН // Фундаментальные исследования. – 2016. – № 3-3. – С. 501-504;URL: https://fundamental-research.ru/ru/article/view?id=40086 (дата обращения: 25.04.2024).