Известно, что для нелинейных стохастических систем, а также для систем, на входах которых действуют сигналы с нелинейной структурой, использование корреляционных функций часто не приводит к желательным результатам, поскольку корреляционные функции не являются исчерпывающими характеристиками связи между случайными процессами [4, 5] и могут обращаться в нуль даже тогда, когда существует детерминированная зависимость между входным и выходным процессами системы.
Для устранения негативных явлений, возникающих в этих случаях, предлагается использовать аппарат дисперсионных функций [4, 5].
Однако, как показано в [2, 3], дисперсионные меры связи хотя и являются более мощным статистическим аппаратом, чем корреляционные функции, также как и корреляционные функции не являются состоятельными мерами связи между случайными процессами. Поэтому в работе предлагается состоятельный метод, основанный на использовании обобщенных корреляционных функций и функциональной корреляции и идеях статистической линеаризации.
Метод многоступенчатой идентификации
Рассмотрим линейный статический многомерный объект, выходная переменная Y которого зависит от вектора наблюдаемых входных факторов 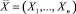 и вектора ненаблюдаемых или наблюдаемых с большим запаздыванием входных факторов Z = (Z1, ..., Zm). Согласно поставленной задаче, будем предполагать, что значения ненаблюдаемых входных факторов Z1, ..., Zm, соответствующие синхронным значениям сигнала на выходе объекта, достаточно хорошо представляются в виде некоторых функций от наборов косвенных показателей или же процессами авторегрессии.
и вектора ненаблюдаемых или наблюдаемых с большим запаздыванием входных факторов Z = (Z1, ..., Zm). Согласно поставленной задаче, будем предполагать, что значения ненаблюдаемых входных факторов Z1, ..., Zm, соответствующие синхронным значениям сигнала на выходе объекта, достаточно хорошо представляются в виде некоторых функций от наборов косвенных показателей или же процессами авторегрессии.
Ввиду того, что процесс авторегрессии является частным случаем регрессии одного случайного процесса относительно других случайных процессов, будем считать в дальнейшем, что значения ненаблюдаемых входных переменных представимы в виде функций от некоторых наборов наблюдаемых косвенных показателей.
Как известно, наилучшим приближением зависимой случайной величины через независимые переменные в смысле критерия минимума средней квадратической ошибки является условное математическое ожидание. Поэтому будем полагать, что ненаблюдаемые (наблюдаемые с запаздыванием) входы Z1, ..., Zm достаточно хорошо представляются своими условными математическими ожиданиями относительно векторов косвенных показателей  т.е.
т.е.
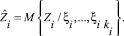 (1)
(1)
Ограничения типа линейности на регрессию 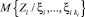 не накладываются.
не накладываются.
Ненаблюдаемые входы Z1, ..., Zm, прогнозируемые с помощью уравнений (1), будем называть факторными переменными, а уравнения (1) – промежуточными факторами. Факторы Z1, ..., Zm, используя терминологию предикторного управления, можно называть предикторными факторами.
Частными случаями уравнения (1) являются уравнения линейной регрессии:
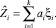
Уравнения регрессий (1) можно получить, используя известные методы.
Выбор наборов косвенных переменных для прогноза соответствующих ненаблюдаемых параметров осуществляется на основе алгоритмов выбора информативных переменных методов факторного анализа. В наборы косвенных переменных могут входить и наблюдаемые входные факторы – 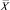 и наоборот.
и наоборот.
Уравнение основной математической модели для прогнозирования выходной переменной объекта будем искать в классе линейных моделей вида
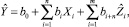 (2)
(2)
где b0, bi, i = 1, ..., n, ..., n + m – неизвестные параметры.
При решении практических задач во многих случаях удобнее пользоваться нормированными статистическими характеристиками анализируемых случайных величин и процессов. При этом упрощаются вычисления и становится более наглядным анализ влияния отдельных входных факторов на прогнозируемую выходную величину.
Выразим все переменные и зависимости между ними в стандартизованном масштабе по формулам
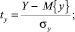
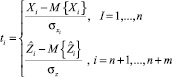 . (3)
. (3)
При этом уравнение модели (2) примет вид
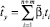 , (4)
, (4)
где 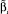 – коэффициенты стандартизированной модели ‒ находятся из условия квадратичного минимума функционала
– коэффициенты стандартизированной модели ‒ находятся из условия квадратичного минимума функционала
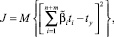 (5)
(5)
которое приводит к системе из n + m линейных уравнений относительно n + m неизвестных параметров модели (4)
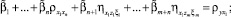
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
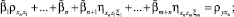 (6)
(6)
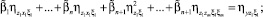
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
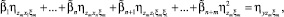
где 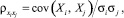 i, j = 1, ..., n – коэффициент корреляции между случайными величинами Xi, Xj;
i, j = 1, ..., n – коэффициент корреляции между случайными величинами Xi, Xj; 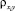 – коэффициент корреляции между Xi и Y;
– коэффициент корреляции между Xi и Y;
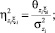
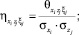
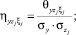
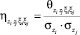
– нормированные значения соответствующих дисперсионных функций;
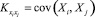 – корреляционный момент случайных величин Xiи Xj, а – корреляционный момент между сигналами на выходе и i-м входе объекта;
– корреляционный момент случайных величин Xiи Xj, а – корреляционный момент между сигналами на выходе и i-м входе объекта; 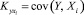 ;
; 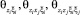 – различные типы дисперсионных функций (моментов).
– различные типы дисперсионных функций (моментов).
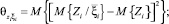
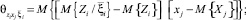
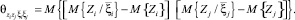
Решение системы (6) может быть записано в виде
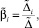 i = 1, ..., n + m, (7)
i = 1, ..., n + m, (7)
где
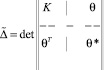 (8)
(8)
– определитель системы (6); 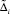 – определитель, получающийся из
– определитель, получающийся из 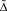 заменой в нем соответствующего столбца столбцом свободных членов системы (6).
заменой в нем соответствующего столбца столбцом свободных членов системы (6).
В (8) T – знак транспонирования, а матрицы K, θ и θ*равны

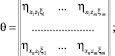
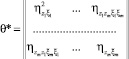 .
.
При записи определителя 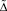 в форме (8) учтено то обстоятельство, что матрицы системы уравнений (6), а также матрицы K и θ*являются симметричными. Этот факт легко следует из определений и свойств корреляционных и дисперсионных функций.
в форме (8) учтено то обстоятельство, что матрицы системы уравнений (6), а также матрицы K и θ*являются симметричными. Этот факт легко следует из определений и свойств корреляционных и дисперсионных функций.
Следует заметить, что матрица системы (6) отличается от корреляционной матрицы системы нормальных уравнений, получающейся в результате применения МНК к стандартной задаче идентификации тем, что ее элементами являются не только коэффициенты корреляции, но и нормированные дисперсионные функции, а на главной диагонали, кроме единиц, стоят элементы 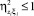 . Дело в том, что нормированная взаимная дисперсионная функция
. Дело в том, что нормированная взаимная дисперсионная функция 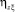 равна единице в том и только том случае, когда между случайными величинами Z и
равна единице в том и только том случае, когда между случайными величинами Z и 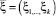 существует точная функциональная зависимость. Очевидно, что при решении практических задач надо стремиться к тому, чтобы мера определенности прогноза случайной величины Z при помощи набора косвенных показателей ξ1, ..., ξk была близка к единице, т.е.
существует точная функциональная зависимость. Очевидно, что при решении практических задач надо стремиться к тому, чтобы мера определенности прогноза случайной величины Z при помощи набора косвенных показателей ξ1, ..., ξk была близка к единице, т.е. 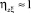 .
.
Используя матричные обозначения, уравнение модели представим в виде
YM = VB, (9)
где 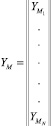 – [N×1] матрица значений выходной переменной модели; N – число наблюдений;
– [N×1] матрица значений выходной переменной модели; N – число наблюдений;
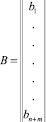 – [(n + m)×1] матрица параметров модели;
– [(n + m)×1] матрица параметров модели;
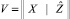 – [N×(n + m)] блочная матрица наблюдаемых и прогнозируемых значений входных сигналов;
– [N×(n + m)] блочная матрица наблюдаемых и прогнозируемых значений входных сигналов;
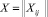 – [N×n] матрица значений наблюдаемых факторов X1, ..., Xn;
– [N×n] матрица значений наблюдаемых факторов X1, ..., Xn;
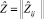 – [N + m] матрица прогнозируемых значений входных факторов Z1, ..., Zm.
– [N + m] матрица прогнозируемых значений входных факторов Z1, ..., Zm.
Функционал (4) можно записать в виде
J = ETE, (10)
где 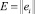 – [N×1]матрица невязок,
– [N×1]матрица невязок,
E = YM – Y.
Минимизируя (10) по всем компонентам вектора параметров B и используя при этом стандартную процедуру минимизации квадратичного функционала, получим уравнение для определения вектора параметров модели (9).
VTVB = VTY, (11)
где
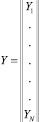 – [N×1] матрица значений выходной переменной модели; N – число наблюдений; T – знак транспонирования.
– [N×1] матрица значений выходной переменной модели; N – число наблюдений; T – знак транспонирования.
Решение матричного уравнения (11) в предположении невырожденности матрицы (VTV) имеет вид
B = (VTV)–1VTY. (12)
Предикторные переменные в факторном анализе
В классическом факторном анализе основным предположением связи переменных является равенство
X = LF + E, (13)
где X – вектор-столбец наблюдаемых переменных размерности p×1; L – p×k матрица факторных нагрузок; F – k×1 вектор-столбец факторов (k < p); E – p×1 вектор-столбец остатков, которые предполагаются независимыми как между собой, так и с факторами. Дисперсии остатков (или остаточные дисперсии) образуют матрицу V.
Уравнение (13) постулирует основные предположения факторного анализа о том, что множество наблюдаемых коррелированных переменных X, которые подчиняются многомерному нормальному распределению с корреляционной матрицей C размерности p×p, можно описать меньшим числом гипотетических переменных или факторов F и множеством независимых остатков E.
Рассмотрим модель объекта с выходом Y и входом X = (X1, ..., Xp). Если p велико, возникает желание уменьшить размерность модели, выразив ее входы через меньшее количество k < p некоторых переменных F. Таким образом, получаем схему факторного анализа. Построение модели Y непосредственно по переменным F невозможно, т.к. они являются гипотетическими (ненаблюдаемыми). Однако эти переменные могут быть выражены через наблюдаемые переменные X следующим образом: 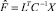 – для некоррелированных факторов и
– для некоррелированных факторов и 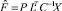 – для коррелированных факторов, где P – оцененная корреляционная матрица факторов.
– для коррелированных факторов, где P – оцененная корреляционная матрица факторов.
Модель объекта будем искать в виде
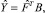 (14)
(14)
где B – вектор-столбец неизвестных коэффициентов размерности k×1. Коэффициенты вектора определим из условия минимума среднеквадратического критерия, т.е. таким образом, чтобы функционал 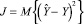 принимал минимальное значение.
принимал минимальное значение.
Подставляя (14) в 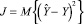 и дифференцируя полученное выражение по В, придем к уравнению
и дифференцируя полученное выражение по В, придем к уравнению
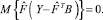 (15)
(15)
Решая (15) с учетом 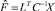 , получим
, получим
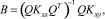 (16)
(16)
где 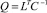 – матрица размерности k×p, а матрицы Kxx и Kxy определяются соответственно формулами:
– матрица размерности k×p, а матрицы Kxx и Kxy определяются соответственно формулами:
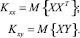 (17)
(17)
Для коррелированных факторов получим
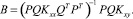 (18)
(18)
Следует отметить, что (16) и (18) получены при условии линейной связи между факторами и входными переменными. Если эта связь нелинейна, то в (16) и (18) вместо (17) будут входить матрицы, элементами которых являются дисперсионные функции.
Заключение
Следует заметить, что в постановке задачи и при выводе конечных результатов предполагалось, что прогнозируемые входные факторы зависят от разных векторов косвенных показателей. В частном случае ненаблюдаемые входные сигналы могут определяться одним и тем же набором косвенных факторов.
Предложенный метод использовался для моделирования загрязнения и хронических заболеваний в Хабаровском крае [1].
Рецензенты:
Гордеев Л.С., д.т.н., профессор кафедры «Кибернетика химико-технологических процессов» Российского химико-технологического университета им Д.И. Менделеева, г. Москва;
Комиссаров Ю.А., д.т.н., профессор, зав. кафедрой «Электротехника и электроника» Российского химико-технологического университета им Д.И. Менделеева, г. Москва.
Работа поступила в редакцию 06.08.2013.



