Исследуется управление КА вектором тяги двигательной установки на внеатмосферном участке спуска с орбиты ИСЗ, обеспечивающее минимум расхода топлива. Решение задач оптимального управления КА сопряжено с большими затратами расчетного времени. Поэтому целесообразно использовать быстродействующие квазиоптимальные алгоритмы решения вариационных задач.
Проведенные исследования посвящены разработке таких алгоритмов для определения оптимального управления КА вектором тяги на внеатмосферном участке спуска с орбиты ИСЗ. Решалась задача минимизации потребной массы топлива (J = ∆mТ = min) при посадке КА баллистического типа в заданную точку поверхности Земли.
Постановка задачи
Движение КА описывается системой дифференциальных уравнений, являющейся частным случаем системы [1]:
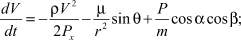
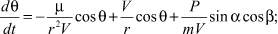(1)
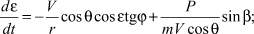
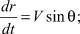
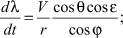
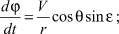
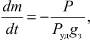
где V – скорость КА; θ – траекторный угол; ε – курсовой угол; r – радиус-вектор, соединяющий центр Земли и центр масс КА; λ и φ – геоцентрические долгота и широта, соответственно; m – масса КА; ρ – плотность атмосферы; μ – произведение постоянной притяжения на массу Земли; Px – приведенная нагрузка на лобовую поверхность КА; Cx – аэродинамический коэффициент лобового сопротивления; P – тяга двигательной установки; Pуд – удельная тяга; gЗ – ускорение свободного падения на поверхности Земли; α – угол между проекцией вектора тяги на плоскость движения и вектором скорости КА; β – угол между вектором тяги и плоскостью движения КА.
Управление КА осуществлялось путем изменения параметров вектора тяги – P, α и β:
0 ≤ P ≤ Pmix; –π ≤ α ≤ π; –π ≤ β ≤ π. (2)
Начальное состояние КА определялось параметрами орбиты ИСЗ и его массой:
V0 = V(t0); θ0 = 0; ε0 = ε(t0);
r0 = r(t0); λ0 = λ(t0);
φ0 = φ(t0); m0 = m(t0). (3)
Концом траекторий является точка на поверхности Земли (hR = 0) c координатами
λR = λ(hR); φR = φ(hR). (4)
Учитывались промежуточные условия при входе КА в атмосферу (hвх = 100 км):
Vвх = V(hвх); θвх = θ(hвх). (5)
Исследования по разработке алгоритмов основывались на теории оптимального управления: для КА, движение которого описывается уравнениями (1) требуется найти законы управления P(t), α(t), β(t), обеспечивающие экстремум функционала J = ∆mT = m0 – mк – min при ограничениях (2), краевых (3), (4) и промежуточных (5) условиях.
Для решения вариационной задачи использовался принцип максимума Понтрягина [4]. Введем в рассмотрение гамильтониан
H = PF1 + F2. (6)
Сопряженные переменные ψi (i = 1, 2, …, 7) определяются соотношениями:
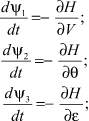
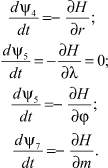(7)
Законы изменения параметров α, β и P определяются из условия
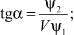(8)
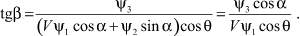(9)
Тяга двигательной установки принимает граничные значения
P = Pmax при F1 > 0, P = 0 при F1 < 0. (10)
Алгоритм расчета оптимальных маневров
Докажем, что число участков полета КА с включенной тягой не превышает двух. Для определения числа переключений исследуем функцию F1, вычисляемую из уравнения [3]:
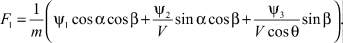
С учетом формул (9) и (10) получим
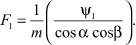(11)
Будем считать, что полет КА при включенной двигательной установке определяется в основном активными силами, а на пассивном участке – гравитационными силами. Предположим, что углы α, β и θ на активных участках полета КА меняются слабо. Тогда уравнения для переменной ψ1, влияющей на функцию F1, имеют вид
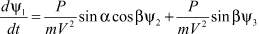при P ≠ 0;
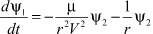при P = 0
В условиях сделанных предположений в обоих случаях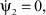 
, т.е. ψ2 = С*.
Покажем, что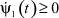 
при t0 ≤ t ≤ tR. Уравнение для ψ1 при P ≠ 0 с учетом (8) и (9) преобразуется следующим образом:
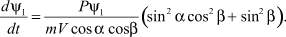
Поскольку выражение ψ1/cos α имеет тот же знак, что и cos β, то справедливо неравенство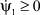 
при P ≠ 0.
Знак переменной ψ1 при P = 0 зависит от знака постоянной ψ2 = С*, который определяется из следующих соображений. Для перевода КА с орбиты ИСЗ на траекторию снижения угол α должен находиться в диапазоне –π ≤ α < –π/2. Тогда из уравнения (11) получим, что ψ1 ≤ 0, а с помощью уравнения (8) определим, что ψ2 = C* ≤ 0. Следовательно,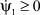 
на пассивном участке полета. Анализ зависимости 
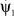показал, что переменная ψ1 скачком меняет свою величину в момент переключения тяги двигателя P. Отсюда заключаем, что переменная ψ1 на всем участке полета КА меняет свой знак не более двух раз, а число переключений тяги двигательной установки КА равно двум. Причем переключения осуществляются с P = Pmax на P = 0, а затем опять на P = Pmax.
Используя допущение об импульсном характере работы двигателей и решая уравнения движения [2], определим начальные углы ориентации вектора тяги α0 и β0:
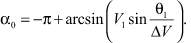, (12)
где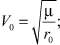 
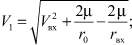
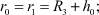
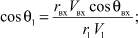
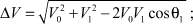
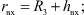
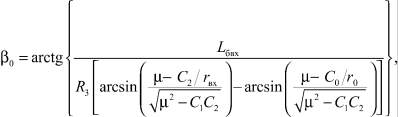(13)
где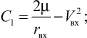 
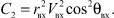
Кроме того, рассмотрен двухимпульсный переход: первый импульс величиной ∆V1 с α0 = π обеспечивает вход КА в атмосферу с заданными значениями Vвх и Lбвх, а с помощью второго импульса ∆V2, подаваемого при r = rвх, корректируется величина θ.
Алгоритм расчета траекторий спуска
Разработан быстродействующий алгоритм расчета траекторий баллистического спуска КА с орбиты ИСЗ в заданную область поверхности Земли. Поскольку параметры точки посадки аппаратов баллистического типа определяются фазовыми координатами при входе КА в атмосферу, задача обеспечения спуска аппарата в заданную область поверхности Земли в данной постановке сводится к нахождению координат схода КА с орбиты λсх и φсх и требуемого бокового смещения траекторий спуска Lбвх при входе аппарата в атмосферу относительно плоскости орбиты.
Пусть граничные условия (3) и (4) принимают такие значения, при которых возможен спуск КА с орбиты ИСЗ в заданную точку поверхности Земли на текущем витке. Найдем зависимость величины Lбк от исходных условий. Пусть в некоторый момент времени tэ КА проходит экватор и характеризуется подспутниковой точкой A с географическими координатами λ = λэ, φ = 0. Конечная точка B имеет координаты φB и λB (рисунок).
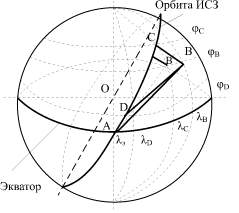
Схема для определения координат схода КА с орбиты: А – положения КА на экваторе; В – точка посадки КА; С – точка пересечения ортогональных плоскостей АОС и ВОС; D – точка схода с орбиты, B′ – уход точки B из за поворота Земли за время t1
Определим угловое расстояние между точками A и B для невращающейся Земли:
∆ν = arccos(cos φв cos Δλ), (14)
где Δλ = λв – λА.
Уточненное значение ∆ν можно вычислить по формуле (14), подставляя в нее величину Δλ, полученную с учетом поворота Земли (рисунок):
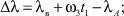
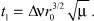(15)
Вычислим наклонение условной орбиты, проходящей через точки А и B:
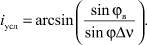
Определим угловое расстояние b между точками B и C:
b = arcsin(sin Δν sinΔi),
где Δi = i0 – iусл.
Между искомой величиной Lбк и угловым расстоянием b имеет место зависимость
Lбк = bR3. (16)
Величину Lвн будем вычислять для импульсной постановки задачи по формуле
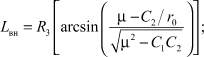
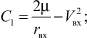
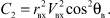
Дальность полета КА баллистического типа в атмосфере может быть вычислена с помощью интегрирования системы (1). С целью сокращения расчетного времени предлагается методика, состоящая в том, что в качестве опорного рассматривается аналитическое решение уравнений, приведенных, в частности, в [5]:
(17)
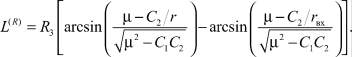
По этим формулам для высот h от hвх = 100 км до hR = 0 вычисляются величины скорости V(R) , траекторного угла θ(R) и дальности атмосферного участка L(R) . Зависимость для скорости полета с учетом влияния аэродинамических сил запишем в виде
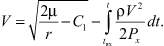(18)
Используя допущение об экспоненциальном характере изменения плотности атмосферы от высоты зависимость (18) преобразуется к виду
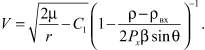(19)
Обоснован интервал изменения аргумента ∆h, на котором сохраняется допущение о кусочном постоянстве аэродинамических сил. Показано, что при значении ∆h = 10 км погрешность вычисления дальности баллистического спуска δL не превышает ~1 %.
Найдем координаты схода КА с орбиты λсх и φсх (рисунок, точка D). Из рассмотрения сферического треугольника DCB получим формулы для расчета координат схода λсх и φсх:
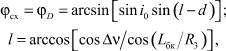
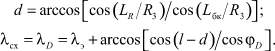(20)
Определим боковое смещение точки входа КА в атмосферу относительно плоскости орбиты Lбвх, которая, являясь входным параметром для расчета траекторий движения КА на внеатмосферном участке, обеспечивает требуемое смещение Lбк на поверхности Земли:
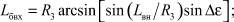
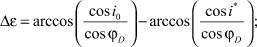
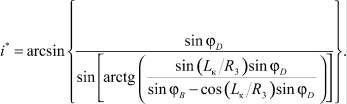(21)
С помощью аналитических формул (18)–(21) вычисляются координаты схода КА с орбиты ИСЗ и требуемое боковое смещение входа КА в атмосферу Lбвх, при которых в сочетании с применением схемы управления вектором тяги на внеатмосферном участке обеспечивается спуск аппарата баллистического типа в некоторую окрестность на поверхности Земли около точки с заданными координатами φR и λR (4).
Представленные преобразования позволяют свести поставленную задачу оптимального управления к безитерационной задаче моделирования уравнений (1). Показано, что в условиях отсутствия случайных возмущающих воздействий отклонения точек посадки КА баллистического типа составляют в среднем 2–3 км, достигая в отдельных случаях ~ 5 км. Для снижения этих отклонений до величин, меньших 1 км, проводится уточненный расчет траекторий, где в формулы для вычисления координат схода с орбиты ИСЗ (20) и для бокового смещения точки входа КА в атмосферу (16), (21) вводятся поправки на величины продольного δL и бокового δLб отклонений точки посадки, вычисленной при первом просчете, относительно заданной с φ = φR и λ = λR.
Заключение
Проведенные исследования оптимального управления вектором тяги, обеспечивающего спуск КА баллистического типа с орбиты ИСЗ в заданную область поверхности Земли при минимальной расходуемой массе топлива, позволяют сделать следующие основные выводы:
- в результате решения вариационной задачи определена структура оптимального управления КА вектором тяги на внеатмосферном участке спуска с орбиты ИСЗ, обеспечивающая минимум потребной массы топлива;
- разработан быстродействующий алгоритм расчета приближенно-оптимальных траекторий КА, спускаемых с орбиты ИСЗ в заданную область поверхности Земли.
Для безитерационного варианта расчета отклонения точек посадки от заданной составляют в среднем 2–3 км, продолжительность вычислений ~10 с. Для одноитерационного варианта отклонения уменьшаются до величины, меньшей 1 км, а продолжительность вычислений увеличится примерно вдвое.
Рецензенты:
Лаврентьев В.Г., д.т.н., начальник отдела, ФГУП «Центральный научно-исследовательский институт машиностроения», г. Королев;
Разумный Ю.Н., д.т.н., профессор, генеральный директор ЗАО «Научно-техническое агентство «Космоэкспорт», г. Москва.
Работа поступила в редакцию 28.05.2014.