В статье рассмотрим постановку задачи и результаты моделирования экономической динамики предприятия для важного частного случая, когда зависимость между выпуском и затратами задается неоклассической производственной функцией степени однородности α (α > 0). Напомним, что если в границах экономической области предприятия его производственная функция является однородной степени ?, то зависимость «выпуск-затраты» задается соотношением [1, 3]:
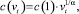(1)
где vt – величина выпуска (в натуральном или стоимостном выражениях) для периода планирования t; c(vt) – совокупные затраты на объем выпуска vt; c(1) – удельные затраты.
Из (1) следует
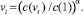(1′)
Выше нами введено понятие производственного капитала как текущих активов, формируемых на основе собственных и заемных средств и авансируемых на покрытие производственных и внепроизводственных затрат (постоянных и переменных) операционной деятельности планового периода t.
Так как производственный капитал расходуется полностью, то соотношение (1’) можно представить в виде
vt = (PKt)α/r, (2)
где PKt – производственный капитал, сформированный в начале периода t и направляемый на финансирование операционной деятельности этого периода; r = (c(1))α.
Если βt – доля заемного капитала, а Cst – величина собственных средств в производственном капитале для периода t, то
PKt = Cst /(1 – βt). (3)
В свою очередь, собственный капитал Cst предприятия в начале периода t образуется из чистой прибыли и покрытых из выручки затрат операционной деятельности периода (t – 1):
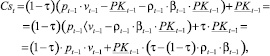(4)
где τ – налог на прибыль; pt–1 – стоимость продукции предприятия для периода (t – 1); ρt–1 – стоимость заёмных средств (в объёме βt–1 •PKt–1), включаемых в производственный капитал предприятия для периода (t – 1).
Производственный капитал PKt, формируемый для периода t, образуется путем выделения собственниками доли γt из собственных средств Cst на начало периода t и краткосрочного кредита, доля которого в его объеме составляет βt:
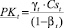(5)
или с учетом (4):
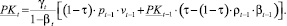(6)
На основании (2) делаем вывод, что
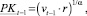(2′)
или 
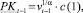(2″)
С учетом (2″) представим (6) в виде
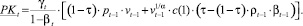(7)
Используя соотношения (2) и (7), получим следующее рекуррентное уравнение, связывающее величины выпусков vt и vt–1 на последовательных интервалах планирования:
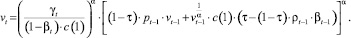(8)
Возвращаясь к формуле (4) расчета величины Cst собственного капитала предприятия по завершении периода (t – 1), определим ту его часть, которая передается в фонд накопления (и в дальнейшем выплачивается акционерам в форме дивидендов).
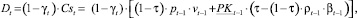(9)
где Dt – абсолютный прирост фонда потребления за период t.
В динамической модели предприятия, задаваемой соотношениями (7)–(9), экзогенными (неуправляемыми) параметрами являются: ставка ? налогообложения прибыли, вектора p и ρ цен соответственно товарного и финансового рынков (по интервалам планирования).
Детерминантами модели являются показатели используемой технологии: α – степень однородности (суммарная эластичность производственной функции или показатель масштаба производства), c(1) – удельные затраты.
Эндогенными (управляемыми) параметрами являются: v1 – объем выпуска в первом плановом периоде, вектора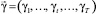 
и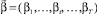 
относительных объемов (долей) соответственно накопления в производственном капитале предприятия собственных средств и финансирования операционной деятельности из заёмных источников.
Таким образом, уравнения (7)–(9) задают возможные траектории изменения результата операционной и финансовой деятельности предприятия в зависимости от проводимой собственниками и менеджментом политики в сфере ее финансирования. Последняя включает выбор структуры производственного капитала (управление долей βt заёмных средств) и его объёма (управление долей γt собственных средств, вкладываемых в производство).
Практическое значение уравнений (7), (8) и (9) заключается в возможности решения следующих задач производственного и финансового планирования:
– выбор оптимального по рыночному критерию (максимум финансового результата операционной деятельности) объёма производства, величины и структуры производственного капитала для очередного интервала планирования, исходя из объема и структуры производственного капитала текущего периода, изменений экзогенных и эндогенных параметров функционирования предприятия;
– определение оптимальной пропорции инвестиций в производственный капитал (затрат на планируемый объём производства) и собственного потребления.
Перечисленные задачи, связанные с исследованием экономической динамики предприятия для абсолютно конкурентных товарных и финансовых рынков и для частного случая линейной зависимости выпуска и затрат (степень однородности производственной функции α = 1), проводились М.А. Халиковым и Р.М. Расуловым [2, 4]. Ими показано, что в этом случае экономическая динамика предприятия корректно описывается однородным разностным уравнением второго порядка. Если соответствующее характеристическое уравнение разрешимо в действительных числах, то динамика выпуска описывается возрастающей или убывающей экспоненциальной функцией, если в комплексных, то периодической волнообразной функцией (растущей или затухающей).
Для исследования экономической динамики предприятия с нелинейной неоклассической производственной функцией, задаваемой уравнениями (7)–(9), рассмотрим отдельно случаи растущей (α > 1) и падающей (α < 1) отдачи от масштаба производства. Не ограничивая общности рассуждений, будем считать заданными и фиксированными: ставку τ налогообложения прибыли, цены p – товарного и ρ – финансового рынков, а также технологические константы: c(1) (удельные затраты) и v1 (выпуск на первом интервале планирования – в натуральных единицах).
Практические расчеты динамики выпуска предприятий с неоклассической производственной функцией для случаев α < 1, α > 1 и различных комбинаций регулируемых параметров γt и βt приведены для следующих рыночных и технологических констант: τ = 0,13; p = 2; c(1) = 1,2; ρ = 0,15; v1 = 16, Cs1 = 0. Характер динамики выпуска для различных комбинаций параметров α, γt, βt представлен в табл. 1.
Таблица 1
Варианты расчетов динамики предприятия с неоклассической производственной функцией на основе уравнений (7)–(9)
|
α |
γt |
βt |
Динамика «выпуск – затраты» |
|
0,8 |
0,1 |
0,1 |
Экспоненциальное падение (табл. 2, рис. 1) |
|
0,8 |
0,1 |
0,5 |
Экспоненциальное падение |
|
0,8 |
0,1 |
0,9 |
Умеренное экспоненциальное падение (табл. 3, рис. 2) |
|
0,8 |
0,4 |
0,1 |
Экспоненциальное падение (табл. 4, рис. 3) |
|
0,8 |
0,4 |
0,5 |
Умеренное экспоненциальное падение |
|
0,8 |
0,4 |
0,9 |
Квазилинейный рост (табл. 5, рис. 4) |
|
0,8 |
0,6 |
0,1 |
Умеренное экспоненциальное падение |
|
0,8 |
0,6 |
0,5 |
Квазипостоянный выпуск (табл. 6, рис. 5) |
|
0,8 |
0,6 |
0,9 |
Заметный экспоненциальный рост (табл. 7, рис. 6) |
|
0,8 |
0,9 |
0,1 |
Квазилинейное падение (табл. 8, рис. 7) |
|
0,8 |
0,9 |
0,5 |
Линейный рост (табл. 9, рис. 8) |
|
0,8 |
0,9 |
0,9 |
Экспоненциальный рост (табл. 10, рис. 9) |
|
1,2 |
0,1 |
0,1 |
Умеренное экспоненциальное падение (табл. 11, рис. 10) |
|
1,2 |
0,1 |
0,5 |
Умеренное экспоненциальное падение |
|
1,2 |
0,1 |
0,9 |
Заметный экспоненциальный рост (табл. 12, рис. 11) |
|
1,2 |
0,4 |
0,1 |
Квазилинейный рост (табл. 13, рис. 12) |
|
1,2 |
0,4 |
0,5 |
Экспоненциальный рост (табл. 14, рис. 13) |
|
1,2 |
0,4 |
0,9 |
Заметный экспоненциальный рост (табл. 15, рис. 14) |
|
1,2 |
0,6 |
0,1 |
Экспоненциальный рост (табл. 16, рис. 15) |
|
1,2 |
0,6 |
0,5 |
Заметный экспоненциальный рост |
|
1,2 |
0,6 |
0,9 |
Сверхсильный экспоненциальный рост (табл. 17, рис. 16) |
|
1,2 |
0,9 |
0,1 |
Заметный экспоненциальный рост (табл. 18, рис. 17) |
|
1,2 |
0,9 |
0,5 |
Заметный экспоненциальный рост |
|
1,2 |
0,9 |
0,9 |
Сверхсильный экспоненциальный рост (табл. 19, рис. 18) |
Таблица 2
α = 0,8; γt = 0,1; βt = 0,1
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
3,592 |
2,404 |
25,056 |
|
3 |
0,511 |
0,505 |
4,143 |
|
4 |
0,104 |
0,142 |
0,845 |
|
5 |
0,029 |
0,051 |
0,233 |
|
6 |
0,010 |
0,022 |
0,082 |
|
7 |
0,004 |
0,011 |
0,035 |
|
8 |
0,002 |
0,007 |
0,018 |
|
9 |
0,001 |
0,004 |
0,010 |
|
10 |
0,001 |
0,003 |
0,007 |
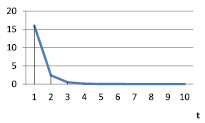
Рис. 1. vt при α = 0,8; γt = 0,1; βt = 0,1
Таблица 3
α= 0,8; γt = 0,1; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
28,322 |
12,542 |
25,056 |
|
3 |
22,178 |
10,313 |
19,960 |
|
4 |
18,223 |
8,814 |
16,401 |
|
5 |
15,564 |
7,769 |
14,008 |
|
6 |
13,713 |
7,020 |
12,342 |
|
7 |
12,388 |
6,472 |
11,149 |
|
8 |
11,417 |
6,063 |
10,275 |
|
9 |
10,693 |
5,754 |
9,624 |
|
10 |
10,145 |
5,517 |
9,131 |
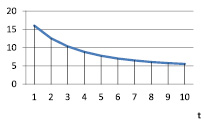
Рис. 2. vt при α = 0,8; γt = 0,1; βt = 0,9
Таблица 4
α = 0,8; γt = 0,4; βt = 0,1
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
14,369 |
7,288 |
16,704 |
|
3 |
6,383 |
3,808 |
8,617 |
|
4 |
3,276 |
2,233 |
4,423 |
|
5 |
1,897 |
1,443 |
2,562 |
|
6 |
1,214 |
1,010 |
1,639 |
|
7 |
0,844 |
0,755 |
1,139 |
|
8 |
0,627 |
0,595 |
0,847 |
|
9 |
0,493 |
0,491 |
0,665 |
|
10 |
0,405 |
0,420 |
0,547 |
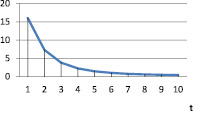
Рис. 3. vt при α = 0,8; γt = 0,4; βt = 0,1
Таблица 5
α = 0,8; γt = 0,4; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
113,288 |
38,019 |
16,704 |
|
3 |
270,300 |
76,231 |
40,545 |
|
4 |
544,136 |
133,420 |
81,620 |
|
5 |
955,919 |
209,407 |
143,388 |
|
6 |
1505,463 |
301,156 |
225,819 |
|
7 |
2171,618 |
403,721 |
325,743 |
|
8 |
2918,915 |
511,484 |
437,837 |
|
9 |
3706,460 |
619,188 |
555,969 |
|
10 |
4495,612 |
722,580 |
674,342 |
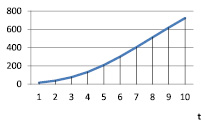
Рис. 4. vt при α = 0,8; γt = 0,4; βt = 0,9
Таблица 6
α= 0,8; γt = 0,6; βt = 0,5
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
36,392 |
15,327 |
11,136 |
|
3 |
34,830 |
14,799 |
11,610 |
|
4 |
33,606 |
14,381 |
11,202 |
|
5 |
32,639 |
14,049 |
10,880 |
|
6 |
31,870 |
13,784 |
10,623 |
|
7 |
31,256 |
13,571 |
10,419 |
|
8 |
30,764 |
13,400 |
10,255 |
|
9 |
30,369 |
13,262 |
10,123 |
|
10 |
30,050 |
13,150 |
10,017 |
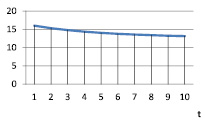
Рис. 5. vt при α = 0,8; γt = 0,6; βt = 0,5
Таблица 7
α = 0,8; γt = 0,6; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
169,932 |
52,586 |
11,136 |
|
3 |
561,799 |
136,874 |
37,453 |
|
4 |
1471,264 |
295,670 |
98,084 |
|
5 |
3197,582 |
550,190 |
213,172 |
|
6 |
5984,757 |
908,432 |
398,984 |
|
7 |
9934,678 |
1362,630 |
662,312 |
|
8 |
14973,941 |
1892,012 |
998,263 |
|
9 |
20880,144 |
2468,549 |
1392,010 |
|
10 |
27343,929 |
3062,977 |
1822,929 |
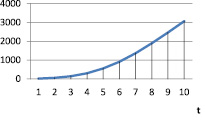
Рис. 6. vt при α = 0,8; γt = 0,6; βt = 0,9
Таблица 8
α = 0,8; γt = 0,9; βt = 0,1
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
32,331 |
13,943 |
2,784 |
|
3 |
28,042 |
12,442 |
2,804 |
|
4 |
24,929 |
11,324 |
2,493 |
|
5 |
22,620 |
10,477 |
2,262 |
|
6 |
20,876 |
9,826 |
2,088 |
|
7 |
19,538 |
9,319 |
1,954 |
|
8 |
18,500 |
8,921 |
1,850 |
|
9 |
17,685 |
8,605 |
1,769 |
|
10 |
17,041 |
8,353 |
1,704 |
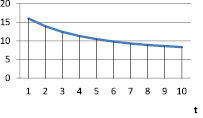
Рис. 7. vt при α = 0,8; γt = 0,9; βt = 0,1
Таблица 9
α = 0,8; γt = 0,9; βt = 0,5
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
54,588 |
21,200 |
2,784 |
|
3 |
72,760 |
26,679 |
4,042 |
|
4 |
92,038 |
32,198 |
5,113 |
|
5 |
111,571 |
37,558 |
6,198 |
|
6 |
130,634 |
42,609 |
7,257 |
|
7 |
148,676 |
47,255 |
8,260 |
|
8 |
165,331 |
51,444 |
9,185 |
|
9 |
180,393 |
55,161 |
10,022 |
|
10 |
193,789 |
58,414 |
10,766 |
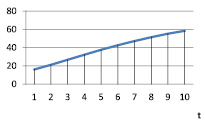
Рис. 8. vt при α = 0,8; γt = 0,9; βt = 0,5
Таблица 10
α = 0,8; γt = 0,9; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
254,897 |
72,736 |
2,784 |
|
3 |
1167,831 |
245,787 |
12,976 |
|
4 |
3980,930 |
655,606 |
44,233 |
|
5 |
10716,430 |
1447,755 |
119,071 |
|
6 |
23882,266 |
2748,625 |
265,359 |
|
7 |
45740,963 |
4622,738 |
508,233 |
|
8 |
77558,514 |
7052,752 |
861,761 |
|
9 |
1,19E + 05 |
9947,053 |
1324,515 |
|
10 |
1,69E + 05 |
13165,810 |
1880,391 |
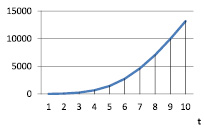
Рис. 9. vt при α = 0,8; γt = 0,9; βt = 0,9
Таблица 11
α = 1,2; γt = 0,1; βt = 0,1
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
3,251 |
3,306 |
25,056 |
|
3 |
0,681 |
0,507 |
5,520 |
|
4 |
0,107 |
0,055 |
0,866 |
|
5 |
0,012 |
0,004 |
0,097 |
|
6 |
0,001 |
18,4E-05 |
0,008 |
|
7 |
4,76E-05 |
5,23E-06 |
3,86E-04 |
|
8 |
1,63E-06 |
9,11E-08 |
1,32E-05 |
|
9 |
3,88E-08 |
1,03E-09 |
3,14E-07 |
|
10 |
7,03E-10 |
8,34E-12 |
5,69E-09 |
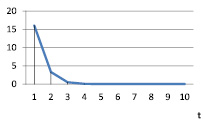
Рис. 10. vt при α = 1,2; γt = 0,1; βt = 0,1
Таблица 12
α = 1,2; γt = 0,1; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
27,992 |
43,794 |
25,056 |
|
3 |
76,554 |
146,468 |
68,898 |
|
4 |
255,815 |
623,007 |
230,233 |
|
5 |
1087,242 |
3536,504 |
978,518 |
|
6 |
6167,162 |
28384,743 |
5550,446 |
|
7 |
49466,851 |
3,45E + 05 |
44520,166 |
|
8 |
6,01E + 05 |
6,92E + 06 |
5,41E + 05 |
|
9 |
1,20E + 07 |
2,52E + 08 |
1,08E + 07 |
|
10 |
4,39E + 08 |
1,89E + 10 |
3,95E + 08 |
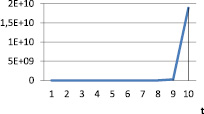
Рис. 11. vt при α = 1,2; γt = 0,1; βt = 0,9
Таблица 13
α = 1,2; γt = 0,4; βt = 0,1
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
13,002 |
17,450 |
16,704 |
|
3 |
14,170 |
19,348 |
19,130 |
|
4 |
15,699 |
21,880 |
21,194 |
|
5 |
17,736 |
25,329 |
23,944 |
|
6 |
20,510 |
30,153 |
27,688 |
|
7 |
24,384 |
37,112 |
32,919 |
|
8 |
29,967 |
47,529 |
40,456 |
|
9 |
38,314 |
63,827 |
51,723 |
|
10 |
51,351 |
90,707 |
69,324 |
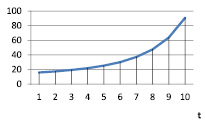
Рис. 12. vt при α = 1,2; γt = 0,1; βt = 0,9
Таблица 14
α = 1,2; γt = 0,4; βt = 0,5
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
22,899 |
34,415 |
16,704 |
|
3 |
49,092 |
85,941 |
36,819 |
|
4 |
122,172 |
256,655 |
91,629 |
|
5 |
363,592 |
949,992 |
272,694 |
|
6 |
1341,222 |
4549,707 |
1005,917 |
|
7 |
6402,668 |
29690,376 |
4802,001 |
|
8 |
41660,661 |
2,81E + 05 |
31245,496 |
|
9 |
3,93E + 05 |
4,16E + 06 |
2,95E + 05 |
|
10 |
5,80E + 06 |
1,05E + 08 |
4,35E + 06 |
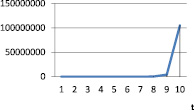
Рис. 13. vt при α = 1,2; γt = 0,4; βt = 0,5
Таблица 15
α = 1,2; γt = 0,4; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
111,967 |
231,149 |
16,704 |
|
3 |
1614,415 |
5683,304 |
242,162 |
|
4 |
39636,839 |
2,65Е + 05 |
5945,526 |
|
5 |
1,84Е + 06 |
2,65Е + 07 |
2,77Е + 05 |
|
6 |
1,85E + 08 |
6,68E + 09 |
2,77Е + 07 |
|
7 |
4,65E + 10 |
5,09E + 12 |
6,98E + 09 |
|
8 |
3,54E + 13 |
1,46E + 16 |
5,31E + 12 |
|
9 |
1,01E + 17 |
2,05E + 20 |
1,52E + 16 |
|
10 |
1,43E + 21 |
1,96E + 25 |
2,14E + 20 |
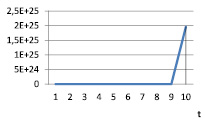
Рис. 14. vt при α = 1,2; γt = 0,4; βt = 0,9
Таблица 16
α = 1,2; γt = 0,6; βt = 0,1
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
19,503 |
28,386 |
11,136 |
|
3 |
34,448 |
56,180 |
20,669 |
|
4 |
67,855 |
126,731 |
40,713 |
|
5 |
152,298 |
334,361 |
91,379 |
|
6 |
399,733 |
1064,405 |
239,840 |
|
7 |
1265,875 |
4244,746 |
759,525 |
|
8 |
5022,601 |
22186,915 |
3013,561 |
|
9 |
26128,417 |
1,61E + 05 |
15677,050 |
|
10 |
1,88E + 05 |
1,72E + 06 |
1,13E + 05 |
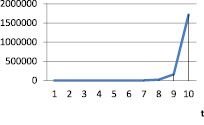
Рис. 15. vt при α = 1,2; γt = 0,6; βt = 0,1
Таблица 17
α = 1,2; γt = 0,6; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
167,951 |
376,011 |
11,136 |
|
3 |
3938,205 |
16570,685 |
262,547 |
|
4 |
1,73E + 05 |
1,55E + 06 |
11552,966 |
|
5 |
1,62E + 07 |
3,61E + 08 |
1,08E + 06 |
|
6 |
3,77E + 09 |
2,49E + 11 |
2,51E + 08 |
|
7 |
2,6E + 12 |
6,36E + 14 |
1,74E + 11 |
|
8 |
6,64E + 15 |
7,79E + 18 |
4,43E + 14 |
|
9 |
8,14E + 19 |
6,27E + 23 |
5,43E + 18 |
|
10 |
6,55E + 24 |
4,84E + 29 |
4,37E + 23 |
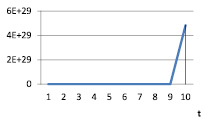
Рис. 16. vt при α = 1,2; γt = 0,6; βt = 0,9
Таблица 18
α = 1,2; γt = 0,9; βt = 0,1
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
29,255 |
46,176 |
2,784 |
|
3 |
83,767 |
163,182 |
8,377 |
|
4 |
293,733 |
735,403 |
29,373 |
|
5 |
1313,953 |
4438,929 |
131,395 |
|
6 |
7877,403 |
38075,197 |
787,740 |
|
7 |
67172,104 |
4,98Е + 05 |
6717,210 |
|
8 |
8,75Е + 05 |
1,09Е + 08 |
87513,411 |
|
9 |
1,90Е + 07 |
4,36E + 08 |
1,90Е + 06 |
|
10 |
7,60E + 08 |
3,65E + 10 |
7,60Е + 07 |
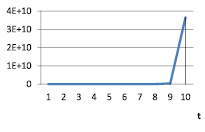
Рис. 17. vt при α = 1,2; γt = 0,9; βt = 0,1
Таблица 19
α = 1,2; γt = 0,9; βt = 0,9
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
251,926 |
611,660 |
2,784 |
|
3 |
9607,058 |
48316,004 |
106,745 |
|
4 |
7,58Е + 05 |
9,13Е + 06 |
8419,042 |
|
5 |
1,43E + 08 |
4,91E + 09 |
1,59Е + 06 |
|
6 |
7,7E + 10 |
9,3E + 12 |
8,55E + 08 |
|
7 |
1,46E + 14 |
7,96E + 16 |
1,62E + 12 |
|
8 |
1,25E + 18 |
4,17E + 21 |
1,39E + 16 |
|
9 |
6,53E + 22 |
1,92E + 27 |
7,26E + 20 |
|
10 |
3E + 28 |
1,2E + 34 |
3,34E + 26 |
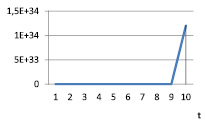
Рис. 18. vt при α = 1,2; γt = 0,9; βt = 0,9
Расчеты динамики «выпуск – затраты» для предприятия с неоклассической производственной функцией, основанные на уравнениях (7)–(9) и отраженные в табл. 1–19 и рис. 1–18, позволяют сделать следующие выводы, часть из которых согласуется с выводами работ [2, 4], полученными для частного случая линейной производственной функции.
1. Масштаб производства (степень однородности производственной функции), являясь неуправляемым фактором модели «выпуск – затраты», существенно влияет на экономическую динамику предприятия, что подтверждается сопоставительным анализом таблиц (табл. 3–12, табл. 4–13, табл. 5–15, табл. 8–18) и графических иллюстраций динамики выпуска (рис. 2–11, рис. 3–12, рис. 4–14, рис. 7–17).
2. Выбор управляемых параметров модели «выпуск – затраты» (γt – темп накопления собственных средств в производственном капитале, βt – доля заемных средств в производственном капитале) является корректным, что отмечено и в цитируемых работах.
В нашем случае пороговым значением показателя γt является 0,4, что подтверждается сравнительным анализом динамики выпуска для значений темпа накопления соответственно меньших и больших этого значения.
3. Аналогично случаю линейной производственной функции важную роль в улучшении динамики выпуска играет фактор налогового щита: с ростом финансового рычага (доли заемных средств) динамика выпуска существенно улучшается.
В целом проведенные теоретические обоснования модели «выпуск – затраты» и осуществленные на ее основе практические расчеты убедительно демонстрируют актуальность постановки задачи оптимизации структуры производственного капитала предприятия на основе корректного определения управляемых параметров, в качестве которых предложено использовать темп накопления собственных средств и коэффициент долга.
Рецензенты:
Тихомиров Н.П., д.э.н., заведующий кафедрой «Математические методы в экономике», РЭУ им. Г.В. Плеханова, г. Москва;
Харченко С.Г., д.ф.-м.н., профессор кафедры национальной безопасности факультета национальной безопасности, Российская академия народного хозяйства и государственной службы при Президенте РФ, г. Москва.
Работа поступила в редакцию 01.10.2014.