При использовании количества информации в процессе оценки состояния технического объекта желательно определиться с понятием «информация». Существует множество определений, относящихся к данному понятию. Например, в [9] информация определяется, как результат выбора – «запомненный выбор». Если обратиться к классической теории информации, в основе которой лежат работы К. Шеннона, то в ней информация определяется как мера или количество неопределённости (информационной энтропии). Само же понятие информации К. Шеннон связывает со снятием неопределенности или с результатом выбора из возможных альтернатив. Как отмечено в [8], информация тесно связана со структурой объектов, поэтому любое их взаимодействие сопровождается изменением зафиксированной в ней информации. Например, структура технической системы в результате взаимодействия между её элементами меняет свое содержание, что свидетельствует об изменении информации, количество которой можно определить через её меру. Следовательно «результат выбора» (через количественную меру информации) уместен в задачах выбора наиболее информативной структуры из альтернатив.
Отмечая упомянутые в работах [8, 9] и К. Шеннона определения информации, их значимость будет обоснована далее при определении количества информации, содержащейся в простейшей структуре технической системы.
Структура системы и состояние её элементов. Оценка состояния технической системы (например, трубопроводных систем, систем электроснабжения, компьютерных сетей и др.) обусловлена задачами (например, проектирования, эксплуатации), в которых вероятностное состояние структуры можно оценить посредством применения теорий вероятности, надежности и информации.
Учет состояний элементов системы и связей между ними, расчет количества присущей ей информации, позволяет на основе конечных результатов осуществить выбор из имеющихся альтернатив. При этом информацию целесообразно рассматривать как процесс, взаимосвязь, отношение между элементами системы. При этом важна та информация, которая указывает на наличие отклонений параметров системы от заданных условий (или значений) под воздействием сторонних факторов [1].
На практике важно уметь численно оценивать степень неопределенности разнообразных состояний (структурных изменений) системы чтобы иметь возможность сравнить их между собой. При этом энтропия является важным показателем неопределенности, определение величины которой может служить мерой структурного состояния системы. Рост энтропии во времени означает развитие хаотических процессов в системе, что свидетельствует о старении элементов системы, понижении уровня надежности, отсутствии должного управления и организационного поведения [5].
Далее в качестве примера определения меры информации рассмотрим структурную надежность системы. В ней каждому элементу присущи два противоположных дискретных состояния: работоспособное и неработоспособное. Если нас не интересует время пребывания элемента в том или ином состоянии, то общее число всевозможных состояний элементов будет равно N = kn, где k = 2 – число возможных дискретных состояний элемента, п – количество элементов в рассматриваемой системе. Данное выражение лежит в основе выражения Хартли для определения меры количества информации в битах: I = log2N.
Условие о наличии противоположных и равновероятных состояний позволяет переписать это выражение в иной форме:
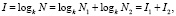 (1)
(1)
где N1 и N2 – количество состояний относящихся к работе и отказу элементов системы соответственно.
Из-за наличия противоположности состояний (работа и отказ), в (1) информация разделена на качественные составляющие. Тем самым учет качественного признака направлен на разделение информации по составляющим с целью последующего выбора. Поэтому процесс определения количества информации должен идти отдельно по каждому из противоположных состояний, поскольку при их слиянии утрачивается смысл оценки уровня надежности через меру информации [2]. Поскольку важнейшей практической задачей является сохранение высокого уровня надежности элемента или системы, то на практике вероятность работоспособного состояния всегда будет выше противоположной вероятности. По этой причине выражение (1) при учете в нем равновероятных состояний малопригодно и может быть использовано только для грубых оценочных расчетов. Устранение данного недостатка приводит нас к необходимости использования формулы Шеннона (при наличии многообразия соотношения противоположных состояний элемента) в следующем виде:
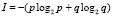 , (2)
, (2)
где, p и q – вероятность нахождения элемента в работоспособном и неработоспособном состоянии, p + q = 1. Из (2) вытекает формула Шеннона для n элементов:
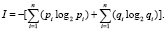 (3)
(3)
Однако выражение (3) малопригодно, поскольку составляющие информаций не отражают наличия взаимосвязей между элементами, то есть совместных событий (состояний), присущих элементам. По этой причине следует построить математическую модель для того, чтобы вычислить количество информации о состоянии самой системы с учетом вероятностного появления в ней совместных и условных событий.
Далее предложим к рассмотрению модель определения информационной энтропии (как меры неопределенности) с учетом качественного признака, обусловленного наличием противоположных состояний элементов.
Упрощенная модель определения энтропии качественного состояния простейшей системы. При построении модели под простейшей системой будем понимать такую, структура которой состоит из двух элементов соединенных последовательно, либо параллельно. Даже в такой системе, на первый взгляд кажущейся простейшей, при сопоставлении последовательных и параллельных структур, количество вероятных состояний резко отличается между собой. Например, в работах [6, 7] отмечается существенное отличие в определении энтропии для последовательных и параллельных структур из-за многообразия комбинаций их состояний. Если число элементов увеличить, то резко возрастет и количество состояний, что сделает работу по определению энтропии практически невозможной.
При построении математических функций энтропии модели выделим ряд общих свойств:
1) неопределенность состояний структуры системы выражается через вероятностные характеристики системы, полученные на основе статистики;
2) энтропийная характеристика системы зависит от размерности пространства состояний системы и числа элементов системы;
3) энтропийная характеристика разделяет вероятностные состояния системы на два противоположных состояния.
В основу для построения функций энтропии положим результаты исследований, представленные в работах [3, 4]. В них даны математические выражения, с помощью которых величина энтропии наложения и пересечения двух взаимосвязанных событий определяется через геометрическую площадь, образованную, с одной стороны, вероятностью события, с другой – частной информацией, присущей событию.
Предварительно рассмотрим энтропийные характеристики H(p) двух независимых событий с вероятностями p1 и p2:
– совместная энтропия (с учетом совместной вероятности p1p2),
H(p1p2) = – p1p2 log2 p1 – p1p2 log2 p2 = = p2H(p1) + p1H(p2), (4)
где H(p1) = – p1log2 p1, H(p2) = – p2 log2 p2;
– условная энтропия (с учетом условных вероятностей p1/p2 и p2/p1),
H(p1/p2) = H(p1) – p1H(p2); (5)
H(p2/p1) = H(p2) – p2H(p1). (6)
H(p1/p2) + H(p2/p1) = H(p1) + + H(p2) – H(p1∙p2) = p1 log2 p1 + + p2 log2 p2 – p2H(p1) – p1 H(p2). (7)
Выражения (4)–(7) справедливы при условии p1 ≠ p2. Однако они не предусматривают разделение энтропии по качественному признаку. Чтобы устранить этот недостаток (и тем самым выполнить третье свойство искомых выражений), введем условие нормировки меры неопределенности.
Нормировка показателей при построении модели. Прежде дадим пояснения в необходимости нормировки. Рассматривая элемент с двумя состояниями по выражению (1) и с двумя равновероятными состояниями p = q = 0,5 по (2), их элементарное сравнение событий (означающее переход от одного состояния к другому) позволяет получить 1 бит максимума информации. Все остальные элементарные сочетания противоположных событий с вероятностями p + q = 1 дают суммарную информацию меньшую единицы. Придерживаясь условия pi + qi = 1 и pi = qi = 0,5, согласно (3) максимальное количество информации, присущее структуре системы будет равно n, то есть числу её элементов. Тем самым выделим ещё одно свойство информации: максимум информации элементарных сравнений противоположных равновероятных событий по каждому из элементов системы равен числу её элементов.
Из определений, представленных в классической литературе по теории информации, следует: информация I и энтропия H обладают безразмерностью, а присутствие линейности их связи – одинаковостью их единиц. Поэтому далее будем говорить об энтропии, поскольку её важным аспектом является присутствие перед логарифмом вероятности (см. (2) и (3)). Она используется либо для усреднения информации, либо указывает на предположение о вероятном появлении события i, наделенного частной информацией: Ii = log2pi. Рассматривая дискретные случайные события, за неопределенность поведения i-го элемента примем энтропию, равную единице:
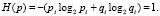 (8)
(8)
Представив (8) как
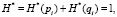 (9)
(9)
можно установить, что составляющие выражения (9) подлежат нормировке. Надстрочный символ (*) означает наличие в формулах нормированной величины энтропии.
В нашей задаче об определении количества информации нормировке будут принадлежать такие переменные, как частная информация, так и энтропия. При этом диапазон разброса этих переменных принимается от 0 до максимального значения.
Простейший вариант нормировки энтропии – линейное преобразование по формуле
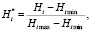 (10)
(10)
где Hi min = 0. Все значения H* по (10) будут укладываться в единичный отрезок [0; 1].
Применение линейной нормировки можно считать приемлемым, когда значения переменной H* плотно заполняют выделенный интервал. Если в статистических событиях данных присутствуют редкие выбросы, выделяющиеся на фоне типичного разброса данных, то эти выбросы установят масштаб нормировки, при котором основная масса значений нормированной переменной сосредоточится вблизи нуля: H*<<1. В таких случаях рекомендуется ориентироваться при нормировке не на экстремальные значения, а на типичные, относящиеся к таким статистическим характеристикам, как среднее и дисперсия. В этом случае большинство данных будет иметь единичный масштаб, и типичные значения всех переменных будут сопоставимы.
Тем не менее, возьмем на вооружение линейную нормировку и покажем энтропийные характеристики H*(p) для независимых событий.
Пусть система состоит из двух элементов, для каждого из которых определены на основе статистических данных вероятности работоспособного pi и неработоспособного qi состояний с условием: pi + qi = 1. Сумма вероятностей разнообразия событий:
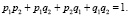 (11)
(11)
Это выражение является основанием для построения функции определения суммарной энтропии двух независимых элементов:
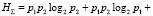
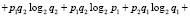
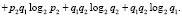 (12)
(12)
Выражение (12) перепишем в виде:
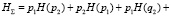
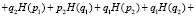
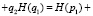
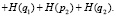 (13)
(13)
В (12) вероятности «перемешаны», то есть имеются произведения вероятностей, относящихся к противоположным событиям. Поэтому применение (13) неудобно для получения, например энтропий, относящихся к разнообразным событиям. Однако можно воспользоваться принципом определения искомых вероятностей событий через вероятности, относящиеся только к одному из противоположных событий. Так, на основе теорем сложения и умножения вероятностей, выражение (11) можно переписать в следующем виде:
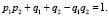 (14)
(14)
Представление (14) в такой форме (с выделением вероятностей событий, рассчитываемых отдельно по каждой из составляющих: р1р2; q1 + q2 – q1q2), наталкивает на мысль о преобразовании выражения (13), которое было бы удобным для расчетов совместных и условных энтропий.
Учитывая вышеизложенные предпосылки, применив нормировку с условиями H*(рi) + H*(qi) = 1 и pi + qi = 1, выражение (13), с учетом преобразований запишем в виде
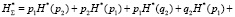
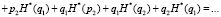
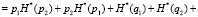
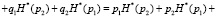
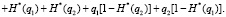 (15)
(15)
В (15) первые два слагаемых не подлежали преобразованиям, поскольку они позволяют определить совместную энтропию двух событий с вероятностями p1 и p2 (см. работы [3, 4]). Остальные четыре слагаемых относятся к вычислению условной энтропии. Выражение для определения условной энтропии можно получить иным путем:
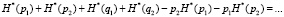
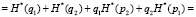
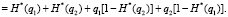 (16)
(16)
В (15) и (16) слагаемые, позволяющие рассчитывать величины совместной и условной энтропий, выделены в отдельные группы по качественному признаку. Тем самым, выражения для определения нормированных значений будут выглядеть следующим образом:
– для совместной энтропии
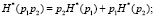 (17)
(17)
– для условной энтропии
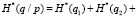
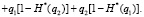 (18)
(18)
Получив нормированные значения энтропии по (17) и (18), можно перейти к определению искомых значений каждой из составляющей энтропии в битах. Например, для составляющих совместной энтропии:
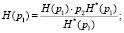
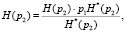 (19)
(19)
для совместной энтропии
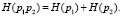 (20)
(20)
Заключение
Рассматривая в процессе разработки проектов и эксплуатации техническую систему, востребованы выражения для определения меры неопределенности информации её структурного содержания. Если природа состояний элементов системы такова, что их вероятности противоположны, то заимствование классических энтропийных характеристик резко усложняет поиск значений энтропии. Расширив свойства информации и введя условие нормировки в построение математических выражений, ориентированных на раздельный учет противоположных событий, решение задачи определения энтропии будет достижимым.
Полученные выражения (17)–(20) (на примере двух элементов) позволяют найти количество совместной энтропии для пересекающихся событий и условной энтропии для всех остальных противоположных событий.
Работа выполнена при поддержке гранта РФФИ № 15-08-01473.
Рецензенты:
Гафнер Ю.Я., д.ф.-м.н., зав. кафедрой общей и экспериментальной физики, ХГУ им. Н.Ф. Катанова, г. Абакан;
Кочетков В.П., д.т.н., профессор, профессор кафедры электроэнергетика Хакасского технического института – филиала Сибирского федерального университета, г. Абакан.



