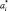В области электроники большое значение имеет коммутация данных, под которой понимается их передача, при которой канал передачи данных может использоваться попеременно для обмена информацией между различными пунктами информационной сети. В частности, при коммутации каналов осуществляется соединение оконечного оборудования данных (ООД) двух или более станций данных и обеспечивается монопольное использование канала передачи данных до тех пор, пока соединение не будет разомкнуто. При этом возможно возникновение ситуации, при которой контакты на одном из каналов, называемом логическим, будут меняться в определенной последовательности. Тогда возникает проблема распознания данных сигналов и их изменение на логическом канале для правильного соединения с другим каналом, называемым физическим. Для решения этой проблемы предлагается выполнить операцию идентификации электрических сигналов, представляющих собой вектор воздействий [2, 7]. Этот процесс может быть широко использован при создании больших интегральных схем (БИС), которые содержат встроенную память. В таких устройствах на одном кристалле интегрированы микроконтроллер, память и интерфейсы взаимодействия с внешними компонентами. Преобразования, о которых идет речь, позволяют выполнить однозначную идентификацию бинарных (двоичных) векторов, координаты которых принимают значения 0 или 1. Для выполнения данных преобразований необходимо разработать математическую модель, учитывая, что данные операции осуществляются на высокой частоте.
Рассмотрим линейное векторное пространство Ln с системой координат, определяемой базисными векторами 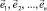 . Тогда любой вектор
. Тогда любой вектор 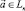 может быть представлен в виде [1, 3, 6]
может быть представлен в виде [1, 3, 6]
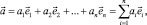 (1)
(1)
где a1, a2, …, an – координаты вектора  в базисе
в базисе 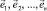 .
.
Линейные однородные преобразования позволяют сформировать вектор 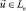 , координаты которого могут быть записаны в виде [1, 3, 6]
, координаты которого могут быть записаны в виде [1, 3, 6]

или U = eA. (2)
Рассмотрим и докажем следующее утверждение.
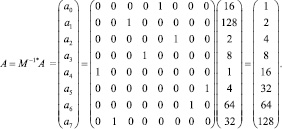
Теорема 1. Пусть двоичный вектор  с базисными координатами, определяемыми вектор-столбцом D, представлен в n-мерном векторном пространстве Ln упорядоченными по возрастанию координатами A = (a0, a1, …, an–1)T, ai = 2i, где
с базисными координатами, определяемыми вектор-столбцом D, представлен в n-мерном векторном пространстве Ln упорядоченными по возрастанию координатами A = (a0, a1, …, an–1)T, ai = 2i, где 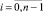 . Тогда его можно преобразовать в n-мерный вектор тестовых воздействий с базисными координатами, определяемыми вектор-столбцом D* и координатами A*, распределенными в произвольном порядке следующим образом:
. Тогда его можно преобразовать в n-мерный вектор тестовых воздействий с базисными координатами, определяемыми вектор-столбцом D* и координатами A*, распределенными в произвольном порядке следующим образом:
D* = MD; A* = MA, (3)
где M – мономиальная матрица n-го порядка.
Доказательство. От противного. Предположим, что в указанной матрице M имеется больше одного элемента, отличного от нуля хотя бы в одной из ее строк. Однако координаты двоичного вектора определяются выражением ai = 2i, где 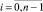 . Все данные числа имеют только одну единицу в двоичной системе счисления, а для вычисления всех новых координат применяется аналогичная формула
. Все данные числа имеют только одну единицу в двоичной системе счисления, а для вычисления всех новых координат применяется аналогичная формула 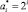 . Получено противоречие. Таким образом, для однозначного соответствия координат векторов и физических контактов ОД требуется использовать мономиальную матрицу n-го порядка.
. Получено противоречие. Таким образом, для однозначного соответствия координат векторов и физических контактов ОД требуется использовать мономиальную матрицу n-го порядка.
Пример расчета 1. Вектор воздействий, заданный в векторном пространстве L8, преобразуется по схеме, изображенной на рис. 1.
|
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Номера координат |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Исходные значения базисных векторов |
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Исходные координаты ai |
⇓ по формулам (3)
|
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Номера выводов ОД |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
Новые значения базисных векторов |
|
32 |
64 |
4 |
1 |
8 |
2 |
128 |
16 |
Новые координаты |
Рис. 1. Схема преобразования вектора в пространстве L8
Новые координаты для приведенного выше примера образуются в результате умножения матрицы M на вектор-столбец исходных координат:
 (4)
(4)
Из теоремы 1 можно сформулировать следствия.
Следствие 1.1. Для того чтобы два или более двоичных вектора, суммарная размерность которых равна n, объединённые операцией конкатенации, были правильно переданы на выводы ОД, достаточно, чтобы векторное пространство тестовых воздействий, поступающих на выводы ОД, имело размерность m ≥ n, а его базисные векторы не соответствовали бы одной и той же координате.
Следствие 1.2. Если векторы из векторного пространства P размерностью n преобразовать при помощи операций, указанных в теореме 1, и по два вектора, взятых из векторных пространств R и S с суммарной размерностью n, преобразовать при помощи операций, указанных в следствии 1.1, то можно получить матрицу тестовых воздействий, в которой первая строка состоит из базисных векторов первого вектора пространства P, вторая – из базисных векторов первых преобразованных векторов, взятых из пространств R и S, третья - из базисных векторов второго преобразованного вектора пространства P и т.д.
Следствие 1.3. Двоичные векторы размерностью s меньше, чем число выводов ОД, можно преобразовать с помощью операций, указанных в теореме 1, и его элементы занести в память тестовых воздействий, но тогда сигналы на остальных r – s выводах ОД будут неопределенные, или им будет присвоено текущее значение соответствующих разрядов буферного блока памяти. Однако применение неопределённых значений сигналов может привести к возникновению необъяснимых отказов ОД или даже к выходу из строя его компонентов. Во избежание этих нежелательных последствий следует перед занесением векторов в память тестовых наборов записать во все разряды буферного блока памяти код нуля. При этом блокируется подача на выводы ОД некорректных воздействий и не выполняется сравнение ответных реакций и эталонных значений по тем выводам, которые не определены в программе теста.
Для описания операции обратной идентификации можно сформулировать и доказать следующее утверждение.
Теорема 2. Пусть базисные векторы реакций ОД представлены в n-мерном векторном пространстве Ln с произвольным порядком распределения координат A* задаются вектор-столбцом D*. Тогда часть или все ответные реакции ОД можно преобразовать в m-мерное векторное пространство для m ≤ n с упорядоченным по возрастанию порядком распределения координат A и базисными координатами, заданными вектор-столбцом D следующим образом:
D = CmD*; A = CmA*, (5)
где Cm – матрица, состоящая из m первых строк матрицы M–1; M–1 – матрица, обратная матрице M; Cm = M–1 при m = n.
Доказательство. Для определения m-мерного векторного пространства достаточно m координат, которые определяются из координат векторного пространства Ln с помощью мономиальной матрицы размера m-го порядка, следовательно, остальные элементы (n – m) столбцов матрицы Cm могут принимать только значение 0. Для обеспечения однозначности преобразований векторов из m-мерного векторного пространства в n-мерное пространство и обратно для n = m необходимо обеспечить соблюдение условия, при котором произведение матриц MCm является единичной матрицей [1, 3].
Из теоремы 2 можно получить следствие.
Следствие 2.1. При n = m все координаты векторного пространства Ln преобразуются в упорядоченные координаты A и образуется вектор реакций со всех контактов ОД.
Пример расчета 2. Сформировать упорядоченный вектор реакции, зафиксированный на всех контактах ОД, приведенных на рис. 1.
Создадим матрицу M–1, обратную матрице M по приведенной на рис. 2 схеме.
Исходные координаты для приведенного выше примера образуются в результате умножения матрицы M–1 на вектор-столбец новых координат:
 (6)
(6)

Рис. 2. Схема определения обратной матрицы M–1
Значения базисных векторов определяются следующим равенством:
 (7)
(7)
Полученные координаты и базисные векторы соответствуют исходным данным на рис. 1.
В качестве основного теоретического результата как важный частный случай можно записать следующее утверждение, а также следствия для практического применения.
Теорема 3. Однозначная идентификация двоичных векторов n-мерного векторного пространства Ln с упорядоченным по возрастанию порядком распределения координат ai = 2i, где 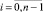 и соответствующих им n терминальных выводов ОД, расположенных в произвольном порядке, возможна тогда и только тогда, когда координаты и базисные векторы преобразуются следующим образом:
и соответствующих им n терминальных выводов ОД, расположенных в произвольном порядке, возможна тогда и только тогда, когда координаты и базисные векторы преобразуются следующим образом:
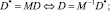
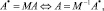 (8)
(8)
где M – мономиальная матрица n-го порядка, которая применяется для преобразования векторов из одного пространства в другое; D – вектор-столбец координат.
Доказательство очевидно, так как это частный случай теорем 1 и 2.
Следствие 3.1. После выполнения поразрядного сравнения ответных реакций ОД и эталонных значений и полученных результатов диагностирования в векторном пространстве Lm можно преобразовать в векторное пространство Ln и в упорядоченном виде передать в компьютер или на экран монитора в удобной для восприятия форме для последующей обработки.
Следствие 3.2. Векторы воздействий, искаженные неисправностями константного типа, возникшими на входных контактах ОД (замыкания контактов на общую шину или шину питания), можно зафиксировать в векторном пространстве Lm, преобразовать в векторное пространство Ln и использовать для формирования соответствующих диагностических сообщений.
Для хранения тестовых векторов в структуре формирователя детермированных тестов предусмотрены запоминающие устройства трех типов: Мb, Мm, Мc.
Запись тестовых наборов в память каналов из буферных блоков BMb, BMm, BMc осуществляется согласно выражению
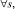
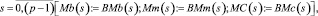
где s – код адреса буферных блоков памяти и памяти каналов, который задается регистром RONk; p – число разрядов данных буферных блоков памяти.
Запись динамического сегмента тестов в память каналов выполняется следующим образом:
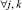
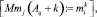
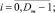
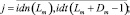
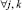
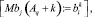
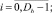
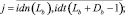
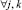
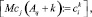
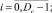
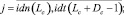
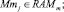
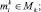
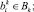
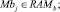
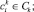
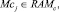
где Aq – адрес начального воздействия; 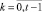 – номер текущего такта диагностирования; t – общее число тестовых наборов; Lm – начальный номер вектора, Lmi – длина вектора; idn – операция идентификации координат векторов и номеров физических контактов ОД, выполняемая с учетом положений, указанных в теореме 3.
– номер текущего такта диагностирования; t – общее число тестовых наборов; Lm – начальный номер вектора, Lmi – длина вектора; idn – операция идентификации координат векторов и номеров физических контактов ОД, выполняемая с учетом положений, указанных в теореме 3.
В результате выполнения указанных выше операций формируется прямоугольная матрица тестовых воздействий:
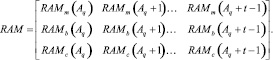
Использование кортежа векторов дает возможность представлять многоразрядные шины в виде булевых векторов с последующей их арифметической и логической обработкой.
Результаты теоретического исследования позволяют спроектировать мультипроцессорный векторный преобразователь, обеспечивающий выполнение указанных преобразований за один период сигнала синхронизации.
Работа выполнена при финансовой поддержке гранта РФФИ (проект 16-08-00393).