С каждым годом увеличивается интенсивность движения и средняя величина нагрузки на ось грузовых автомобилей [15]. Действующие нормативно-технические документы [2, 4], регламентирующие предельные нагрузки на дорожные основания и покрытия, не соответствуют современным условиям эксплуатации. Поэтому возникает необходимость совершенствования как самих технических регламентов, ГОСТов, СНиПов, так и методов проектирования, строительства, ремонта и реконструкции автодорог. Одним из направлений по повышению эксплуатационных показателей асфальтобетонных покрытий является разработка новых добавок, составов, которые бы позволили повысить прочностные свойства дорожных покрытий без отклонения от действующих нормативно-технических документов.
Как в России, так и за рубежом большую популярность имеет щебеночно-мастичный асфальтобетон (ЩМА) [6], который является разновидностью асфальтобетона, отличающейся повышенной каркасностью. По сравнению со смесями, приготовленными по ГОСТ 9128-2013, ЩМА имеет повышенное содержание битума (5,5–7,5 %) и щебня (70–90 %) [14], формирующего прочный скелет, позволяет повысить водо-, морозостойкость, трещиностойкость, устойчивость к старению материала.
ЩМА не может использоваться без стабилизирующих добавок. Как показала практика, от качества стабилизирующей добавки зависит качество и долговечность ЩМА. Их структурирующее действие позволяет гомогенизировать смесь, предотвращая сегрегацию и стекание (отслоение) битумного вяжущего при высоких температурах [5]. В данной работе была использована стабилизирующая добавка «АРМИДОН» на целлюлозной основе. Нами была поставлена задача на основе метода конечных элементов, реализуемого в ПК ANSYS [7-8, 10–13], выполнить анализ напряженно-деформированного состояния (НДС) автодорожного покрытия, изготовленного с применением данной добавки.
Для расчета НДС элементов дорожного полотна необходимо определить физико-механические свойства всех конструктивных слоёв дорожной одежды и основания, для чего была изготовлена серия образцов для каждого конструктивного слоя и проведены испытания этих образцов в соответствии с нормативной документацией [1, 3], определялись следующие параметры: средняя плотность, водонасыщение, сдвигоустойчивость, трещиностойкость, предел прочности на сжатие, определение удельного сцепления, угла внутреннего трения, модуля деформации и коэффициента Пуассона. Для установления действующих эквивалентных напряжений и деформации в покрытии при максимальных эксплуатационных нагрузках использована модель упруго-пластического деформирования материала – Друкера – Прагера (DP). Модель DP задается уравнением
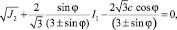 (1)
(1)
где J2 – второй инвариант девиаторной части тензора напряжений; I1 – первый инвариант тензора напряжений; c – удельное сцепление; φ – угол внутреннего трения.
Данный критерий игнорирует влияние инварианта J3 (вводимого углом Лоде θ) на форму сечения. Он может рассматриваться как первая попытка аппроксимировать критерий Мора – Кулона гладкой функцией на основе инвариантов I1 и J2 в сочетании с двумя постоянными материала. В связи с трудоёмкостью вычисления аналитическим путём граничных условий, характерных для дорожного покрытия, как правило, труднодостижимо. Среди различных численных методов механики сплошной среды наиболее совершенным является метод конечных элементов [9].
Для составления общей системы уравнений равновесия всей конечно-элементной модели твердого деформируемого тела используются условия равновесия узлов или вариационные принципы и методы невязок. Для задач статики уравнение в общем виде выглядит следующим образом:
[K]{U} ={P} + {P}q + {P}g + {P}ε0 + {P}σ0, (2)
где [K] – глобальная матрица жесткости КЭ модели; {U} – глобальный вектор, определяющий узловые перемещения элемента; {P} – глобальный вектор заданных внешних узловых сил; {P}q, {P}g, {P}ε0 , {P}σ0 – векторы узловых сил.
Компоненты матрицы [K] являются коэффициентами жесткости модели, они вычисляются путем суммирования соответствующих коэффициентов жесткости КЭ.
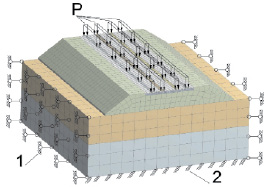
Нами была решена задача с помощью МКЭ в программном комплексе ANSYS 16.0. На конкретном примере было смоделировано земляное полотно для II категории дороги с капитальным дорожным покрытием под воздействием четырёхколёсного автомобиля с максимально возможной нагрузкой на ось в 130 кН согласно [4]. Для определения напряженно-деформированного состояния элементов дорожного полотна при действующих эксплуатационных нагрузках необходимо задать граничные условия конструкции.
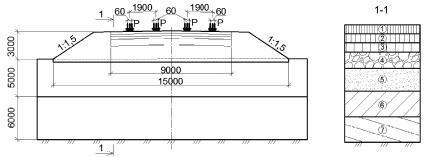
В расчетной схеме (рис. 1) учитывается шарнирное закрепление боковых стенок основания с возможностью вертикальных подвижек частиц грунта. Подошву – нижнюю плоскость основания, в свою очередь, предлагается жёстко закрепить по всем степеням свободы.
Поперечные участки основания (вдоль направления движения) не закрепляются, так как предполагается, что нагрузка действует и за пределами расчетной области.
После назначения граничных условий и приложения действующих эксплуатационных нагрузок выполнялось разбиение модели на конечно-элементную сетку. Разбивка основания и покрытия дорожной одежды была выполнена в условиях пространственной деформации с использованием конечных элементов в форме четырехугольных призм. При создании физической модели основания и дорожного полотна под нагружением использованы конечные элементы: SOLID186, SOLID187, SHELL181, CONTA174, TARGE170, SURF154.
Физико-механические характеристики слоёв, принятые в расчётах, представлены в таблице.
Решение системы дифференцированных уравнений выполнялось методом итераций Ньютона – Рафсона. Сходимость решения оценивалась по узловым усилиям с точностью 0,001.
В результате расчетов многослойной дорожной конструкции МКЭ, реализованном в программном комплексе ANSYS 16.0, получены изополя перемещений (рис. 2, 3) и действующих эквивалентных напряжений (рис. 4).
В результате решения поставленной задачи было определено, что при максимальной прикладываемой нагрузке деформация составит 5 см, а максимальные напряжения, возникающие во втором слое асфальтобетона, составляют 1,5 МПа.
а
б
Рис. 1. Расчётная схема: а – упруго-пластическая модель системы многослойного дорожного покрытия – грунтовое основание: 1 – щебеночно-мастичный асфальтобетон (ЩМА-20) – 0,05 м; 2 – асфальтобетон пористый I марки из крупнозернистой смеси – 0,07 м; 3 – асфальтобетон пористый I марки из крупнозернистой смеси – 0,06 м; 4 – щебеночное основание – 0,34 м; 5 – песок крупный – 2,48 м; 6 – суглинок тугопластичный – 5,0 м; 7 – суглинок полутвердый – 6,0 м; б – 1 – шарнирное закрепление боковых стенок основания; 2 – жесткое закрепление нижней плоскости основания; P – действующая эксплуатационная нагрузка на дорожное полотно, распределенная по колеям
Физико-механические характеристики конструктивных слоёв
|
№ п/п |
Параметры |
ЩМА-2 |
Асфальтобетон пористый I марки (2слоя) |
Щебеночное основание, уложенное методом расклинцовки |
Песок крупный |
Суглинок тугопластичный |
Суглинок полутвёрдый |
|
1. |
Модуль деформации, МПа |
– |
– |
350 |
50 |
32 |
34 |
|
2. |
Коэффициент Пуассона |
0,5 |
0,5 |
0,2 |
0,25 |
0,35 |
0,35 |
|
3. |
Плотность, кг/м3 |
2,42 |
2,31 |
1800 |
1760 |
1970 |
1970 |
|
4. |
Удельное сцепление, кПа |
0,21 |
0,18 |
1 |
2 |
39 |
47 |
|
5. |
Угол внутреннего трения, град. |
0,94 |
0,93 |
70 |
43 |
24 |
26 |
|
6. |
Предел прочности при сжатии, МПа |
1,5 |
1,23 |
– |
– |
– |
– |
|
7. |
Трещиностойкость, МПа |
2,9 |
2,6 |
– |
– |
– |
– |
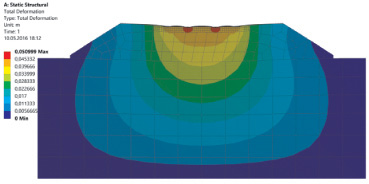
Рис. 2. Распределение деформаций (профиль) – масштаб деформаций х10
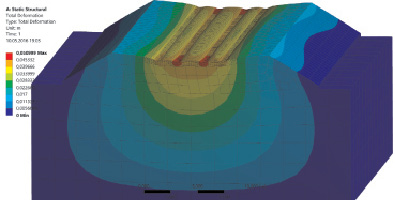
Рис. 3. Распределение деформаций для всего участка – масштаб деформаций х20
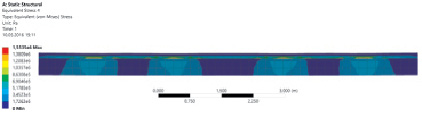
Рис. 4. Распределение эквивалентных напряжений в верхнем слое дорожного полотна – масштаб деформаций х20
Это объясняется тем, что верхний слой выполнен из ЩМА, который является слоем износа, и все нагрузки, действующие на него, передаются нижним слоям дорожного покрытия.
Выводы
В результате численных расчетов были получены максимальные и минимальные значения напряжений в зонах воздействия на конструкцию, области возникновения пластических деформаций в искусственном и грунтовом основаниях, позволяющие прогнозировать деформационные процессы при многократном приложении колесной нагрузки от движения автомобилей. Были получены результаты статических напряжений в дорожной одежде.
Для оценки долговечности дорожного покрытия необходимо также определить усталостные деформации, зная которые, возможно будет установить количество циклов приложения расчётной нагрузки и спрогнозировать срок службы дорожной одежды в зависимости от интенсивности движения.



