Современное промышленное производство характеризуется высоким развитием производственных сил и высокими темпами научно-технического прогресса. Поэтому определение оптимальных вариантов планирования и управления производством представляет собой актуальную проблему. Показатели доходов, затрат, объемов производства, возникающих в процессе производства, необходимо точно определить и оценить, а затем управлять ими для достижения желаемого финансового результата. Эти задачи могут быть решены только с использованием соответствующих экономико-математических моделей и методов.
Существующие методы решения задач оптимального программирования [2, 3, 4, 7] и современные вычислительные средства позволяют реализовывать в практических задачах такие экономико-математические модели.
Основными компонентами математического программирования являются целевая функция и система ограничений. Традиционными требованиями к функциям здесь являются вогнутость целевой и вогнутость функций, определяющих систему ограничений. С математической точки зрения, эти требования делают условия Куна-Таккера достаточными для существования и единственности решения задачи математического программирования, а с экономической – обеспечивают существование равновесия в конкурентном взаимодействии между промышленностью и рынком. Производство стремится максимизировать доход от своей продукции. Этой цели противостоит рынок, который из-за того, что он платит производству, добивается (за счет управления ценами на сырье, которое производство приобретает на рынке) минимизации дохода производства. Отказ от предположений вогнутости функций в задачах оптимизации приводит к тому, что нельзя уже утверждать существования и единственности конкурентного равновесия. Известно [7], что в случае, например, растущей производительности (невогнутость целевой функции) производство стоит перед дилеммой: либо работать в пользу социального оптимума и сталкиваться со значительными убытками, либо сбалансировать бюджет и получать доход, зная, что, скорее всего, ситуация не соответствует оптимальным параметрам.
В данной статье исследуются ситуации, когда вогнутости в названных требованиях нет, но тем не менее оптимальность сохраняется. Для этого в работе рассматривается K – вогнутость [6] функций и приводятся некоторые расширения теоремы Куна-Таккера.
Постановка задачи. Решение в вогнутом случае. Рассмотрим задачу распределения некоторого запаса ресурсов между производствами (см., напр., [1]). В этой задаче нужно определить такой совместный план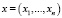 
интенсивностей n производств одной отрасли, что его выполнение приводит к наибольшему значению общего выпуска продукции в условиях ограниченности запаса m видов ресурсов (напр., энергии, материала и т.д.).Таким образом, целевая функция f(x) представляет собой суммарный выпуск продукции всеми производствами, соответствующий уровню производства в промышленности, равном x. Кроме того, промышленности требуется m видов сырья, при этом наличное количество сырьевого материала вида i составляет 
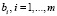. Пусть 
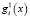– количество сырья i, которое необходимо при уровне производства, равном x, а 
.
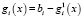Итак, математическая модель задачи является классической задачей математического программирования [2] и имеет вид
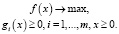(1)
Известно (условия Куна-Таккера, см., напр., [2]), что в случае дифференцируемости функций из (1) и выполнения условия регулярности [2] для оптимальной точки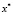 
задачи (1) должны выполняться следующие условия:
1) 
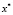– допустимая точка;
2) существуют множители λi ≥ 0, i = 1,..., m, такие, что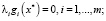 
3) 
.
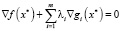Приведенные условия являются необходимыми. Достаточность условий появляется при дополнительных требованиях на функции f(x), g(x),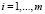 
. Именно [2], если названные функции вогнуты, то точка 
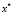, удовлетворяющая условиям Куна-Таккера, является решением задачи (1).
С экономической точки зрения свойство вогнутости функций f(x), g(x),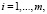 
связано [1] с представлением об убывающей эффективности производства, т.е. о снижении предельных норм выпуска и увеличении предельных норм затрат при расширении масштабов (интенсивностей) производства. Эти свойства в экономической теории обычно принимаются без ограничений, хотя понятно, что на самом деле они должны часто не выполняться. Так происходит в силу причин технологического характера, из-за политического устройства экономики, в силу, наконец, причин экономического характера. Поэтому в исследованиях подобного рода естественно пытаться выделять условия, обобщающие условия вогнутости, что и будет сделано в следующем пункте статьи.
K – вогнутые функции. Приведем определение выпуклого в конусе направлений K множества, или, более коротко, K – выпуклого множества [6].
Определение 1. Множество X в пространстве Rn называется K – выпуклым множеством, если из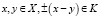 
следует, что отрезок, соединяющий точки x, y, принадлежит множеству X.
Здесь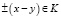 
означает, что по крайней мере один из векторов (x – y), (y – x) принадлежит K.
Заметим, что в этом определении в качестве множества K можно взять произвольное множество.
Будем вновь считать K выпуклым конусом в Rn и рассмотрим скалярную функцию f(x) на некотором множестве X из Rn.
Определение 3. Функция f, определенная на K – выпуклом множестве X в Rn, называется K – вогнутой на X, если
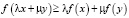(2)
для любых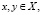 
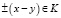и любых 
.
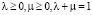В случае выполнения в (2) строгого неравенства пр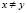и 
и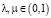 
функция f называется строго K – вогнутой на X.
Пусть функция f(x), определенна и K – вогнута на Rn, множество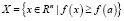 
является K – выпуклым. В самом деле, так как множество X содержит a, то 
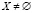. Функция f(x) – K – выпуклая и поэтому для любой выпуклой линейной комбинации 
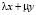точек x, y из X, таких, что 
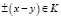, имеем
≥
,
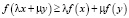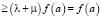что и требовалось доказать.
Перед тем, как сформулировать следующее утверждение, введем один класс множеств. Будем говорить [6], что множество X является l-множеством, если выпуклая оболочка C(X) множества X есть объединение самого X и точек отрезков, соединяющих всевозможные пары точек из X. Пусть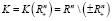 
. Если в этом случае X не содержит положительных точек, то и C(X) их также не содержит. Поэтому из [5, 6] вытекает следующее утверждение.
Утверждение 1. Пусть X –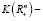 
выпуклое l-множество, не содержащее положительных точек. Тогда существует отделяющая гиперплоскость 
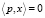с полуположительным вектором нормали 
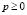, такая, что полупространство 
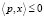содержит множество X.
Введем в рассмотрение множество Y:
,
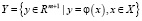где отображение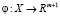 
с некоторой фиксированной точкой 
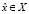определяется по (1) следующими выражениями для компонент 
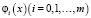вектор-функции φ(x):
.
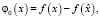
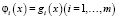Имеет место
Теорема 1. (ср.[2]) Пусть множество X выпукло, а максимизируемая функция f и функции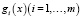 
таковы, что множество Y – 
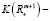выпукло и является l-множеством. Пусть также выполнено условие Слейтера: в X существует точка c, для которой 
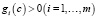. Тогда, если 
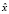– какое-либо решение задачи максимизации при ограничениях (1), то существуют неотрицательные числа 
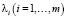, такие, что
(a)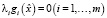 
,
(b)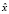 
максимизирует лагранжиан задачи (1) на множестве X при указаных λi.
Доказательство проводится по схеме, предложенной в [5].
Приведем одну из возможных конкретизаций теоремы 1. Рассмотрим случай m = 1, n = 2. Возьмем за X верхнюю полуплоскость, то есть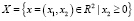 
. Обозначим g(x) = g1(x). Отображение 
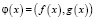будем считать непрерывно дифференцируемым и локально взаимно однозначным в X. В этих предположениях справедлива
Теорема 2. Пусть функции f(x) и g(x) на границе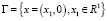 
множества X удовлетворяют следующим условиям:
(1) 
;
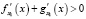(2) 
.
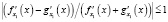Тогда если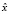 
– какое-либо решение задачи максимизации при ограничениях, то существует неотрицательное число λ, такое, что
(a)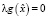 
,
(b)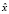 
максимизирует лагранжиан на множестве X при указанном λ.
В заключение приведем одно из возможных следствий утверждения 1 [6].
Теорема 3. Пусть в задаче максимизации с ограничениями (1) функци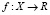и 
и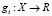 
, 
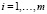являются непрерывно дифференцируемыми на выпуклом множестве X, градиент целевой вогнутой на X функции f при любом 
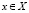принадлежит положительному ортанту 
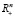, а ограничения gi, 
, 
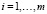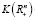вогнуты на X. Предположим, что в допустимой точке 
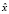выполнены условия Куна-Таккера. Тогда если для любой допустимой точки x задачи (8) разность 
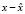не принадлежит множеству 
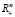, то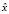 
– решение задачи (1).