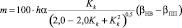Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Мелихова Е.В. 1

---

1 ФГБОУ ВПО «Волгоградский государственный аграрный университет»

В статье рассмотрена проблема математического моделирования конфигурации и параметры контура увлажнения при капельном орошении овощных культур. Это обусловлено не только сложностью математического описания взаимосвязей процессов распространения влаги, но и необходимостью построения модели в трёхмерном пространстве с использованием средств компьютерной математики, поскольку количество моделируемых переменных составляет не менее четырех. Автором разработана математическая модель в виде дифференциального уравнения контура увлажнения при капельном орошении столовой свеклы на светло-каштановых почвах, в которой учитываются водно-физические свойства почвы, глубина увлажнения при заданных порогах влажности. Исследование полученной математической модели позволило численно рассчитывать поливные нормы с учётом глубины увлажнения. Дано сравнение расчетной величины поливной нормы при различных способах и глубине увлажнения.

Статья в формате PDF

556 KB

математическая модель

контур увлажнения

капельное орошение

столовая свекла

1. Мелихова Е.В. Математическое моделирование и оптимизация режима орошения корнеплодов на светло-каштановых почвах Волгоградской области // Известия Нижневолжского агроуниверситетского комплекса: наука и высшее профессиональное образование. – 2009. – № 1. – С. 114–126.

2. Патент РФ № 2343695. 2009. Рогачев А.Ф., Салдаев А.М., Мелихова Е.В. Поливная трубка для капельного орошения / Патент RU № 2343695.2009. Бюл. № 2.

3. Патент РФ № 154632 U1; А01G25/02 Рогачев А.Ф., Бородычев В.В., Мелихова Е.В., Шатырко Д.В. Капельница для комбинированного орошения / Патент RU № 154632 U1; А01G25/02.

4. Шуравилин А.В. Обоснование режимов увлажнения почв при капельном орошении картофеля в аридной зоне / А.В. Шуравилин, Ю.И. Сухарев, М.А. Табук, В.В. Бородычев // Вестник Российского университета дружбы народов. Серия: Агрономия и животноводство. – 2013. – № 3. – С. 45–52.

5. Ясониди О.Е. Водосбережение при орошении. – Новочеркасск, – 2004. – 473 с.

Проблема моделирования контура увлажнения при капельном орошении обусловлена не только сложностью математической зависимости, описывающей зависимость влагопередачи, но и необходимостью построения модели в трёхмерном пространстве. В связи с этим количество моделируемых переменных составляет не менее четырех, что требует использования математического аппарата дифференциальных уравнений в частных производных [1].

Локальность капельного орошения обуславливает особенности техники полива. К элементам техники капельного орошения следует отнести в первую очередь параметры очага (контура или полосы) увлажнения, их наибольший диаметр, ширину, глубину, горизонтальную и вертикальную площади контура увлажнения и влагонасыщенность. Параметры капельного орошения зависят от конструктивных особенностей капельниц, с помощью которых можно задавать режим орошения культур [2, 3].

Возделывание корнеплодов на капельном орошении при экстремальных климатических условиях Нижнего Поволжья обеспечит сохранение плодородия, предотвратит иссушение почв агроландшафтов, создаст условия накопления азота в почве, продуктивность пашни значительно возрастет. Немаловажным является то, что капельное орошение является энерго- и ресурсосберегающим способом полива сельскохозяйственных культур.

Целью исследования являлась разработка математической модели, позволяющей рассчитать водосберегающий режим полива столовой свеклы при капельном орошении на светло-каштановых почвах, за счет дифференциации глубины увлажняемого слоя при поливах в период вегетации свеклы при капельном орошении, с различным уровнем минерального питания. Это позволит получать запланированные урожаи с рациональным использованием материальных, энергетических и природных ресурсов, учитывая водно-физические свойства почвы, получить параметры контура увлажнения для светло-каштановых почв [2].

Обоснование параметров режима орошения было проведено на основе математического моделирования. За основу была взята известная математическая модель влагопереноса С.Н. Новосельского, которая описывается следующим уравнением:

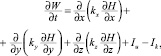(1)

где k_x, k_y, k_z – коэффициенты влагопроводности вдоль осей x, y, z; I_u, I_k – интенсивность источников влагопоступления и влагоотбора корнями растения соответственно.

Функция I_u определяется геометрией увлажнителей, их положением в пространстве и режимом водоподачи. Если источники – пористые и проницаемые сферы исчезающего малого радиуса, то

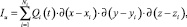(2)

где x_i, y_i, z_i – координаты i-го источника; Q_i(t) – его расход; δ – дельта-функция Дирака; N_i – число точечных источников.

Основными параметрами контура увлажнения являются высота и ширина (рис. 2).

Таким образом, используя встроенные функции Маthcad было получено численное решение дифференциального уравнения влагопереноса в частных производных (рис. 1). Для практического инженерного использования описанной выше методики нами предложено аппроксимирующее выражение вида:

F(x, y) = cos(π Ax) + i·sin(πBy), (3)

где A, B – параметры, характеризующие контур увлажнения; i – мнимая единица.

Классической формулой для определения поливной нормы является зависимость А.Н. Костякова:

m = 100∙γ∙H(β_НВ – β_ПП), (4)

где m – поливная норма, м3/га; Н – глубина расчетного слоя почвы, м; γ – плотность расчетного слоя почвы, m/м3; β_НВ – β_ПП – наименьшая и наибольшая предполивная влагоёмкость расчетного слоя, %.

Расчёт по формуле (4) дает увеличенное значение поливной нормы, что приводит к нерациональному использованию водных ресурсов [1].

При методике расчета поливной нормы для дифференциации глубины увлажняемого слоя предлагается определять поливную норму с учётом эллипсовидной формы образуемого в результате полива контура увлажнения рис. 3. Объём эллипсоида считается по формуле

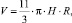(5)

где Н – расчетная глубина увлажняемого слоя почвы, считая от поверхности земли, м; R – наибольший радиус увлажнения почвогрунта, м.

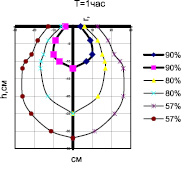
Рис. 2. Распространение влажности почвы в контурах, % от НВ

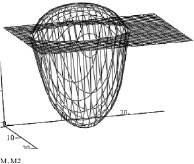
Рис. 3. Пространственная модель контура увлажнения

Подставляя данное выражение в формулу А.Н. Костякова, получаем выражение

m = 0,12∙H∙R∙γ_об∙(β_НВ – β_ПП). (6)

Значение поливной нормы при капельном орошении с учётом эллипсовидной формы контура увлажнения определяют следующим образом:

m = 11,5∙H∙R∙γ_об∙(β_НВ – β_ПП), (7)

где H – расчётная глубина увлажняемого слоя почвы, м; R – радиус увлажнения, м; γоб – объёмная масса, т/м3; 11,5 – коэффициент, полученный в результате действий 11p/3.

Математическая обработка экспериментальных данных показала (рис. 2), что радиус контура увлажнения коррелируется с глубиной увлажнения по формуле

R = 0,431H. (8)

Подставив выражение (8) в формулу (7), получим

m = 4,96∙H2∙γ_об∙(β_НВ – β_ПП)∙n, (9)

где m – значение поливной нормы, л/га; n – количество капельниц на га.

Умножив полученное выражение на количество капельниц, получаем формулу для вычисления поливной нормы:

m = 96,36∙H2∙γ_об∙(β_НВ – β_ПП). (10)

Расчёты по формуле (10) для различной глубины увлажнения приведены в таблице.

Сравнение величин поливной нормы по различным формулам

На основании исследований установлена зависимость поливной нормы и глубины увлажнения. Для сравнения значения поливной нормы, рассчитанной по формуле, предложенной нами, в таблице представлены различные зависимости поливной нормы при капельном орошении и формулы, принятой за основу [4, 5].

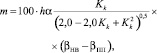(11)

где a – объёмная масса расчётного слоя почвы, т/м³; Kk – увлажняющий участок, выраженный в частях от площади питания растения.

На рис. 3 представлена пространственная модель контура увлажнения полученного решения (3) дифференциального уравнения (1). Как показали исследования, глубина увлажнения и радиус контура увлажнения находятся в корреляционной зависимости.

Таким образом, исследование контура увлажнения позволило создать математическую модель распространения контура увлажнения при капельном орошении и численно рассчитывать поливные нормы с учётом глубины увлажнения.

Рецензенты:

Рогачев А.Ф., д.т.н., профессор, зав. кафедрой «Математическое моделирование и информатика», ФГБОУ ВПО «Волгоградский государственный аграрный университет», г. Волгоград;

Бородычев В.В., д.с.-х.н., профессор, директор Волгоградского филиала ГНУ ВНИГиМ, г. Волгоград.

Библиографическая ссылка